Introduction

RESCU is a density functional theory (DFT) solver based on the Kohn-Sham (KS) formalism. The code is mostly written in the MATLAB programming language with certain key routines written in C. The Kohn-Sham equation and all related quantities are discretized on regular grids in real space and reciprocal space. Using a purely real space implementation allows RESCU to achieve a linear scaling in the Hamiltonian-wavefunction products due to the local nature of finite-differencing and fully separable pseudopotentials. The locality of the Hamiltonian operator leads to a high parallelizability. More parallelism is obtained using specialized hardware such as GPUs and libraries like ScaLAPACK.

Our researchers have generated and tested various sets of norm-conserving pseudopotentials. Both LDA (local density approximation) and GGA (generalized gradient approximation) pseudopotentials are available; they have been tested by comparing with projector augmented wave band structure calculations and all-electron total energy equation of states. The Troullier-Martins scheme is used to produce transferable pseudopotentials including partial core charge where appropriate. Our pseudopotential database also includes an atomic orbital basis set for each element.

RESCU also performs KS-DFT calculations within the atomic orbital framework. It can then tackle larger problems by representing the wavefunctions as linear combinations of atomic orbitals. This procedure significantly alleviate the memory requirements in large systems. Numerical atomic orbitals are generally transferable, but cannot suit all chemical environments. In such cases, RESCU uses Chebyshev filtering to create a minimal adaptive basis set which has all the advantages of real space and plane wave methods: systematic convergence, vanishing Pulay forces, etc.

RESCU implements many levels of DFT:

1. LDA, GGA, meta-GGA (mGGA);

2. Hartree-Fock exchange, hybrid functionals;

3. degenerate spin;

4. collinear spin;

5. non-collinear spin;

6. spin-orbit interaction.

RESCU implements the Perdew-Wang LDA functional and the Perdew–Burke–Ernzerhof GGA functional. Additional semi-local functionals are evaluated using the LibXC functional library.

RESCU includes tools to determine the Bravais lattice and the system symmetries. The first Brillouin zone (BZ) grid is then reduced accordingly. This can greatly accelerate solid state computations, density of states computations in particular. Using numerical atomic orbitals in conjunction with real space grids also makes it possible to compute quantities such as projected density of states (PDOS) and Mulliken charge matrices. The density of states is evaluated using the tetrahedron method or Gaussian smearing. In addition, reciprocal lattice variations (similar Bravais lattices may have different first BZ) are recognized and vertices of the irreducible BZ are labelled, which is convenient in band structure calculations.

Additional RESCU tools comprise structure relaxation and frozen phonon calculation. The structure relaxation is perform using either the steepest descent or the non-linear conjugate gradient algorithm. For frozen phonon calculations, the RESCU DFT solver is used to obtained the inter-atomic force constants, which are used to calculate the dynamical matrices, band structure and DOS. A summary of RESCU’s features can be found in Fig. 1.

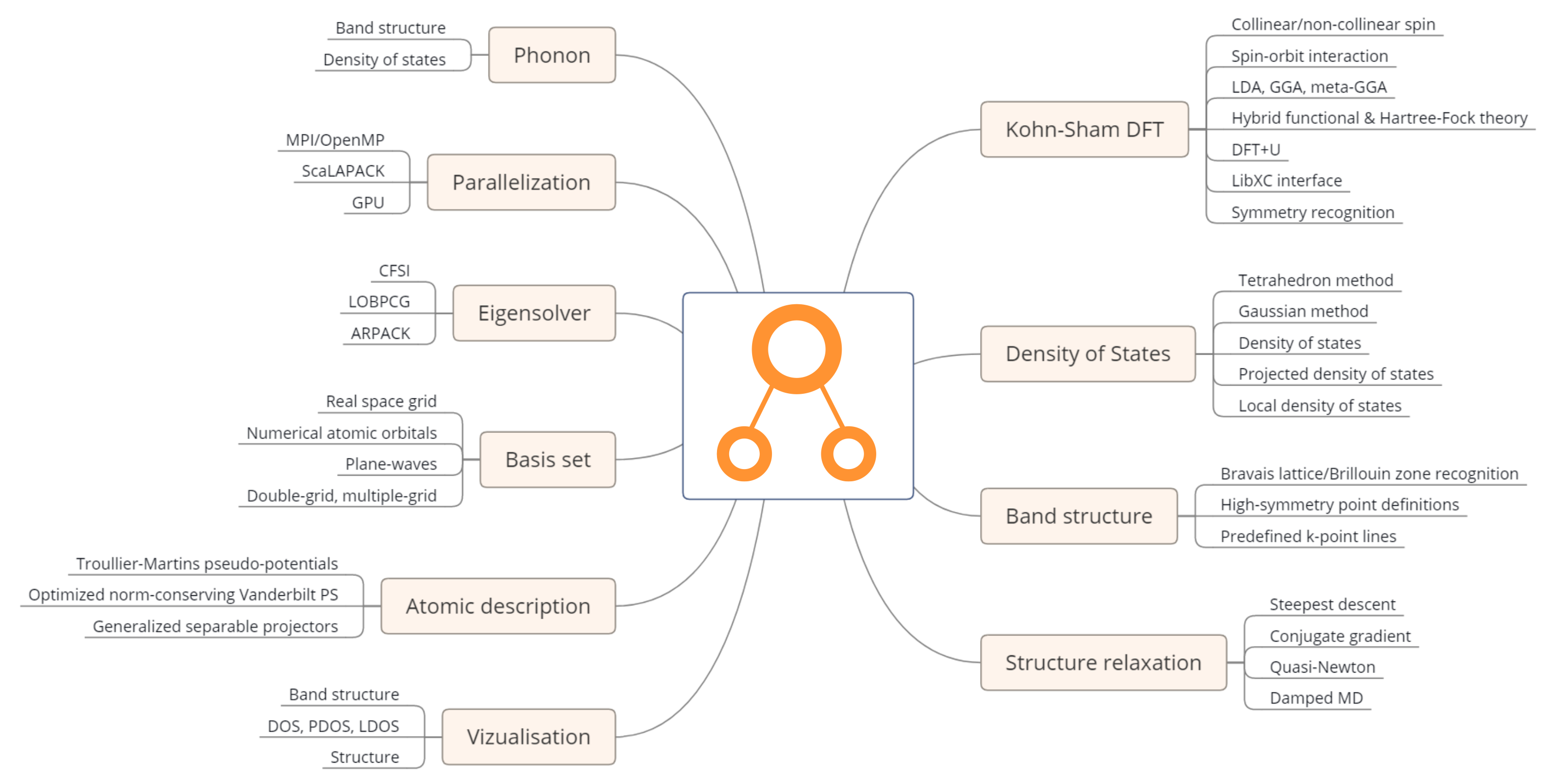
Fig. 1 RESCU features.