Introduction
Electronic devices work by transport of electrons. For nano-structures, transport features are sensitive to the material, chemical and atomic details of the system. They are also sensitive to the external fields and quantum effects, and device operation is often under nonlinear and non-equilibrium conditions. In order to make quantitative predictions for quantum transport, it is necessary for theoretical methods to include the microscopic physics.
Nanodcal is a state-of-the-art software tool for quantitative modeling of charge/spin quantum transport from atomistic first principles without relying on any phenomenological parameter. The input of nanodcal is the atomic structure of the device, while the output is the self-consistently solved quantum transport features at the nonlinear and non-equilibrium level. The User Reference manual of nanodcal summarizes its application.
You are reading the Theoretical Background manual which presents the theoretical formulation implemented in nanodcal. Nanodcal is based on combining a real space self-consistent field (SCF) theory with the Keldysh non-equilibrium Green’s function formalism (NEGF). The basic idea of the NEGF-SCF is to self-consistently calculate the Hamiltonian and electronic structures of the device; calculate the non-equilibrium quantum statistical properties and density matrix by NEGF; and account for the open device transport boundary conditions and electrostatic boundary conditions by real space numerical techniques. The first implementation of NEGF-SCF reported in literature can be found in Ref. [TGW01] and a subsequent implementation to deal with spin polarized transport is in Ref. [WHL06]. When a system is actually at equilibrium, the NEGF-SCF reduces properly to the familiar equilibrium theory: NEGF reduces to the equilibrium Fermi-Dirac distribution while the SCF reduces to the conventional density functional theory (DFT).
There are several excellent DFT packages which have seen wide range of applications in materials science, condensed matter physics, quantum chemistry and theoretical biology. These applications largely fall into two categories and are mostly in equilibrium. First, DFT solves problems involving isolated, finite sized atomic structures - frequently seen in quantum chemistry. Second, DFT solves problems involving periodic atomic structures - such as in solid state physics. However, quantum transport involves open device structures neither periodic nor finite, and the flow of electric current in these open systems is inherently a non-equilibrium problem. Therefore non-equilibrium transport problems are beyond the scope of most DFT packages.
NEGF is a many-body theoretical formalism commonly seen in the theoretical physics literature for analyzing nonlinear and non-equilibrium quantum transport problems. So far, the overwhelming majority of NEGF analysis started from phenomenological Hamiltonian where atomic and material properties of the device structure are coded into adjustable parameters. By carefully picking these parameters, qualitative physics can hopefully be investigated to gain insights. However, deeper understanding of nano-electronic devices often requires quantitative methods.
Based on the extensive literature of both DFT and NEGF, and driven by the desire to quantitatively investigate non-linear and non-equilibrium quantum transport, significant research has been carried out in academia to seek an atomic based NEGF formalism that can make quantitative predictions for nano-electronic device operation. Since the problem cannot be solved exactly, diverse approaches and efforts can be found in the literature. Nanodcal follows a particular and we believe the most practical and fruitful approach, by extending the self-consistent DFT to open systems and in combination with NEGF. Using nanodcal, it is possible to predict a wide range of quantum transport properties of nanostructures from atomic first principles [TGW01, WHL06] without any phenomenological parameter.
In this Theoretical Background manual, we present the formulation in nanodcal. To save space, we shall leave out the derivation but cite the relevant references. This manual is organized as follows. The next subsection presents the transport model and nanodcal design principle. Section 2 presents the DFT of nanodcal. Section 3 presents the NEGF-SCF formulation of nanodcal. Section 4 presents formulation of various post analysis of nanodcal, while the last section briefly summarizes some future issues.
Device model in nanodcal
Nanodcal calculates quantum transport features from atomistic point of view. A few example atomic structures can be found in Fig. 14 in Section NEGF-DFT in NanoDCAL. The device Hamiltonian of nanodcal is quantum such that quantum transport equations are solved instead of the classical or semi-classical equations. We use Fig. 12 to explain the device model in nanodcal. In nanodcal, a device has two or more electrodes extending to electron reservoirs at infinity where bias voltage \(V_{b}\) is applied and current collected. The electrodes are made of metallic materials and hence maintains equal-potential all the way to near the device scattering region, and \(V_{b}\) is dropped across the scattering region.
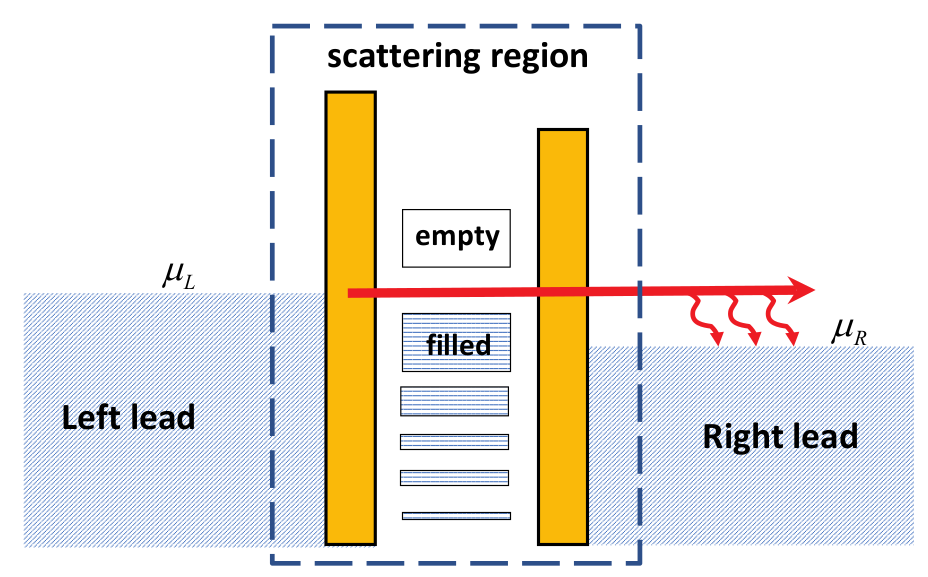
Fig. 12 Schematic plot of a two-probe device model. \(\mu_{L},\mu_{R}\) are the electrochemical potentials of the left/right electrodes, and \(\mu_{L}-\mu_{R}=eV_{b}\) where \(V_{b}\) is the bias voltage and \(e\) the electron charge. The dash-lined box indicates the device scattering region which has some quantum levels. The tunnel barriers indicate coupling of the scattering region to the semi-infinitely long electrodes.
The semi-infinitely long electrodes are periodic structures away from the scattering region, and each electrode is at its own equilibrium state with a well defined electrochemical potential \(\mu\). However, the entire system - scattering region plus the electrodes, are at non-equilibrium because each electrode has its own \(\mu\). In Fig. 12, electrons come from the left electrode with \(\mu_{L}\), they traverse the scattering region, transmit to the right electrode or reflect back to the left electrode. The transport model assumes coherent quantum scattering and all the dissipative effects occur inside the electrodes far away from the scattering region. Therefore, when electrons having \(\mu_{L}\) traverse to the right electrode which is at \(\mu_{R}\), they become hot electrons since \(\mu_{L}>\mu_{R}\). Subsequently some dissipative events occur in the right electrodes (more precisely, at the right reservoir) so that the hot electrons equilibrate to \(\mu_{R}\). In Fig. 12 the dissipate events are indicated by the three small wiggly arrows. In the literature, this quantum transport model is the Landauer-Büttiker model. Within this model, transport problem becomes an electron scattering problem by the potential of the device scattering region.
In Fig. 12, the potential or Hamiltonian of the scattering region must be calculated. Nanodcal calculates it using a self-consistent field (SCF) method presented in Section 3. Once the Hamiltonian is obtained, one can calculate the energy levels (see Fig. 12). In equilibrium, nanodcal populates these quantum levels by Fermi-Dirac distribution function to construct the density matrix which is needed by the SCF, as described in Section 2. In non-equilibrium, nanodcal constructs the density matrix by NEGF as described in Section 3.
Importantly, the Hamiltonian of the scattering region has contributions from the infinitely large number of free electrons in the device electrodes. These degrees of freedom are integrated out and their influence is accounted for by a self-energy term that gets added to the Hamiltonian of the scattering region. Such a mathematical procedure reduces the calculation on an infinitely large device model to one that focuses on the scattering region. The price to pay is the inclusion of the dissipative self-energy terms which make the Hamiltonian non-Hermitian. Another important point is that the alignment of the \(\mu_{L},\mu_{R}\) to the energy level spectrum of the scattering region (see Fig. 12) is critical for quantitative predictions. Nanodcal calculates this alignment self-consistently, see Section 3.
Taylor, J., Guo, H., & Wang, J. (2001). Ab initio modeling of quantum transport properties of molecular electronic devices. Physical Review B, 63(24), 245407.
Waldron, D., Timoshevskii, V., Hu, Y., Xia, K., & Guo, H. (2006). First Principles Modeling of Tunnel Magnetoresistance of Fe/MgO/Fe trilayers. Physical Review Letters, 97(22), 226802.