5. Valence band maximum tutorial

5.1. Introduction

In this tutorial, you will see how to compute the valence band maximum of diamond. This VBM is obtained invoking Janak’s theorem

\(\frac{d E(n_i)}{dn_i} = e_i\)

where \(n_i\) is the occupation number of the highest occupied state \(i\) with the eigenvalue \(e_i\). This is calculated by finite difference, i.e. by removing a small fractional charge from the diamond unit cell.

\(e_i = \frac{E[Q=N] - E[Q=N-\delta N]}{\delta N}\)

where \(\delta N = 10^{-3}\) is usually a good value.

5.2. Write an input file template

We will perform 4 total energy calculations to obtain 3 VBM values. We first write an input file template like scf_base.input. Note the lines

info.savepath = './results/scf_fxfacx'
info.outfile = 'fscf_fxfacx.out'
atom.nvalence = 2 * 4 - 1 / xfacx

The tag xfacx will be replaced by the inverse fraction of removed electrons. For example, setting the tag to 100 will set the valence to 2 * 4 - 1 / 100 = 7.99, removing 0.01 electron. The first two lines set the name of the result file and standard output log file respectively.

5.3. Perform the calculations

As mentioned above, we will perform 4 total energy calculations. To generate the 4 corresponding input files, one may run the script genall.sh. The tag values are set to 10, 100, 1000, 10000. Our template uses the pseudopotential file C_SZDP.mat which should be at the root of the tutorials directory. One can perform the calculations one by one, or run them in parallel using the script runall.sh. Before using runall.sh, modify the script considering that N is the number of simultaneous calculations and NCORE is the total number of cores you want to use.

5.4. Determine the equilibrium volume

The last step is to extract the equilibrium volume from the equation of states. This is done with the script read_vbm.m. It will list the files that match the pattern results/scf_f*.mat, there should be 4 in total. Then it will compute the VBM values using finite differences. Finally, it will print

vbm = 10.126067 eV

The smallest difference value is printed, but make sure that it is converged. This is readily seen on a plot of the VBM as a function of difference.

figure()
semilogx(x,vbm); hold on
xlabel('\Delta N')
ylabel('\Delta E / \Delta N (eV)')
saveas(gcf,'eos_vbm.png')

which gives

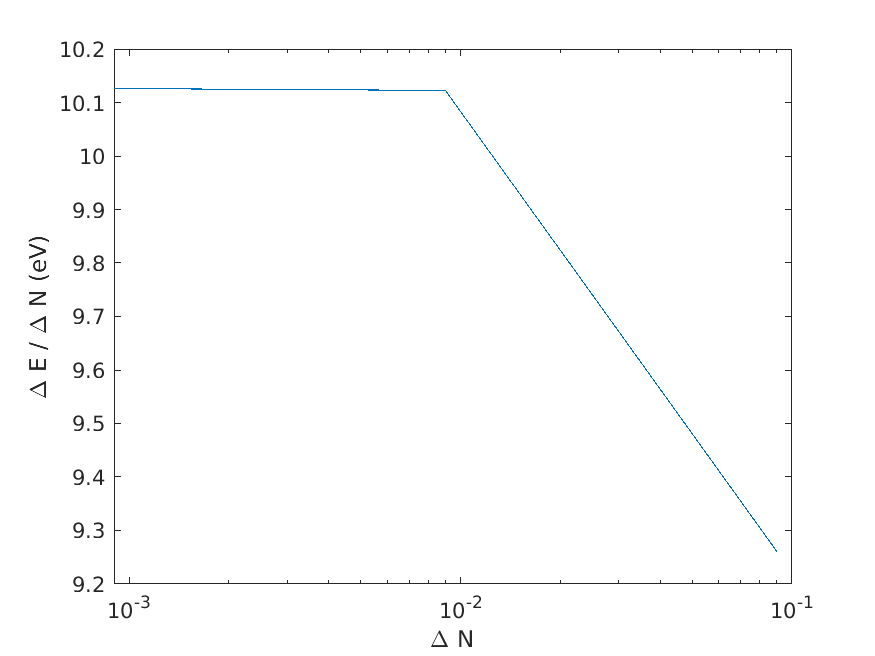
Fig. 5.4.1 VBM versus occupancy difference