3. Equation of states tutorial
3.1. Introduction
In this tutorial, you will see how to compute the lattice constant of diamond using total energy calculations. We will use a Birch–Murnaghan equation of state fit to extract the equilibrium volume. The Birch–Murnaghan equation of state reads
3.2. Write an input file template
We will perform 7 total energy calculations around the experimental
value of 3.57 A. We first write an input file template like
(scf_base.input). Note the lines
info.savepath = './results/scf_fxfacx'
info.outfile = 'fscf_fxfacx.out'
aa = 3.57 * xfacx / 100
There is a tag xfacx that will be replaced by numbers, and hence we
call this a template. For example, setting the tag to 100 will make
the lattice constant 3.57 * 100 / 100 = 3.57. The first two lines
set the name of the result file and standard output log file
respectively. The third line sets the lattice constant. As for the rest
of the file, you should define the structure and set the resolution and
k-sampling to sensible values. If the accuracy parameters are not
stringent enough, the fit will not be of good quality.
3.3. Perform the calculations
As mentioned above, we will perform 7 total energy calculations around
the experimental value of 3.57 A. To generate the 7 corresponding input
files, one may run the script genall.sh. The important thing here is
{94..106..2} which means that the tag will be replace by
94, 96, 98, 100, 102, 104, 106. Depending on the material, this
range may be too large or too narrow. You should adjust it so that the
energy varies by at least a few meV. Our template uses the
pseudopotential file C_SZDP.mat which should be at the root of the
tutorials directory. One can perform the calculations one by one, or
run them in parallel using the script runall.sh. Before using
runall.sh, modify the script considering that N is the number of
simultaenous calculations and NCORE is the total number of cores you
want to use.
3.4. Determine the equilibrium volume
The last step is to extract the equilibrium volume from the equation of
states. This is done with the script read_eos.m. It will list the
files that match the pattern results/scf_f*.mat, there should be 7
in total. Then it will call the function eosfit to do the fit.
Finally, it will print
v_eq = 5.647781 ang^3/atom
From that we can deduce the lattice constant for the conventional
diamond lattice. Multiply by 8 and take the cubic root, and get 3.56
A. You may also plot the EOS as follows
figure(); hold on
plot(avol,anrg)
xlabel('volume (A^3/atom)')
ylabel('energy (eV/atom)')
saveas(gcf,'eos_diamond.png')
which gives
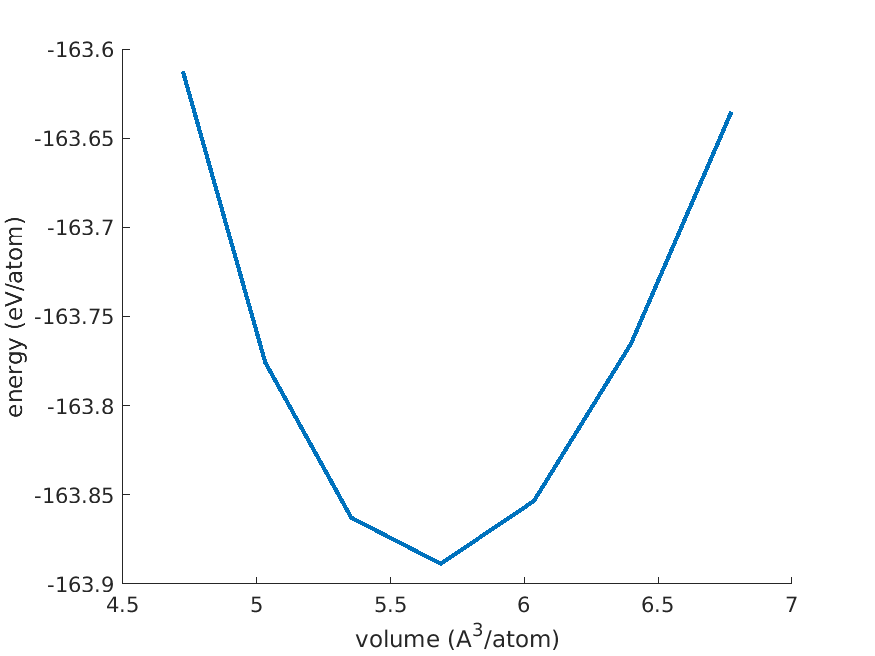
Fig. 3.4.1 Diamond equation of states