2.4. Projected density of states calculation
More information can be extracted by projecting the wavefunctions onto
atomic orbitals and then computing the density of states using only
certain components. Such a function is called a projected density of
states (PDOS). It is possible to compute the fraction of the density of
states originating from a specific atom, atoms certain species, orbitals
with a specific angular momentum for example. In the case of graphene, I
expect the PDOS to be equivalent for both atoms by symmetry. I thus look
at its angular momentum components. Copy the following input file and
save it to a text file named c2_pdos.txt.
info.calculationType = 'dos'
info.savepath = 'results/c2_pdos'
atom.element = [1 1]
la = 4.648725932
atom.xyz = [1 1/sqrt(3) 0;1 -1/sqrt(3) 0]/2*la
domain.latvec = [1/2 sqrt(3)/2 0; 1/2 -sqrt(3)/2 0; 0 0 4]*la
domain.lowres = 0.3
dos.range = [-0.70,0.20]
dos.projL = [0,1]
dos.projM = [-1,0,1]
element.species = 'C'
element.path = './C_TM_LDA.mat'
kpoint.gridn = [45,45,1]
kpoint.shift = [0,0,0]
LCAO.status = 1
rho.in = 'results/c2_scf'
Then pass it to RESCU and execute the program as follows
rescu -i c2_pdos.txt;
New keywords are highlighted in blue. I will briefly explain each of them.
info.savepathwas changed not to overwrite the dos results;dos.projLtells RESCU to decompose the DOS in its \(L=0\) and \(L=1\) components (otherwise known as \(s\) and \(p\));dos.projMtells RESCU to decompose the DOS in its \(M=-1\), \(M=0\) and \(M=1\) components. RESCU will compute the PDOS for every combinations ofdos.projLanddos.projM.
The \(L\) and \(M\) values refer to the real spherical harmonics entering the atomic orbital definitions. Ill-defined \(L\) and \(M\) combinations are ignored. In the current example, \((L,M)=(0,0)\) give the \(s\)-PDOS, \((L,M)=(0,-1)\) give the \(p_y\)-PDOS, \((L,M)=(0,1)\) give the \(p_z\)-PDOS, \((L,M)=(0,0)\) give the \(p_x\)-PDOS. The position of the graphene lattice with respect to the \(x\)-axis and \(y\)-axis is arbitrary as the problem is periodic along these dimensions. I thus sum up the \(p_x\) and \(p_y\) PDOS in Fig. 2.4.2. The \(p_{z}\) states makes up for most of the DOS around the Fermi energy.
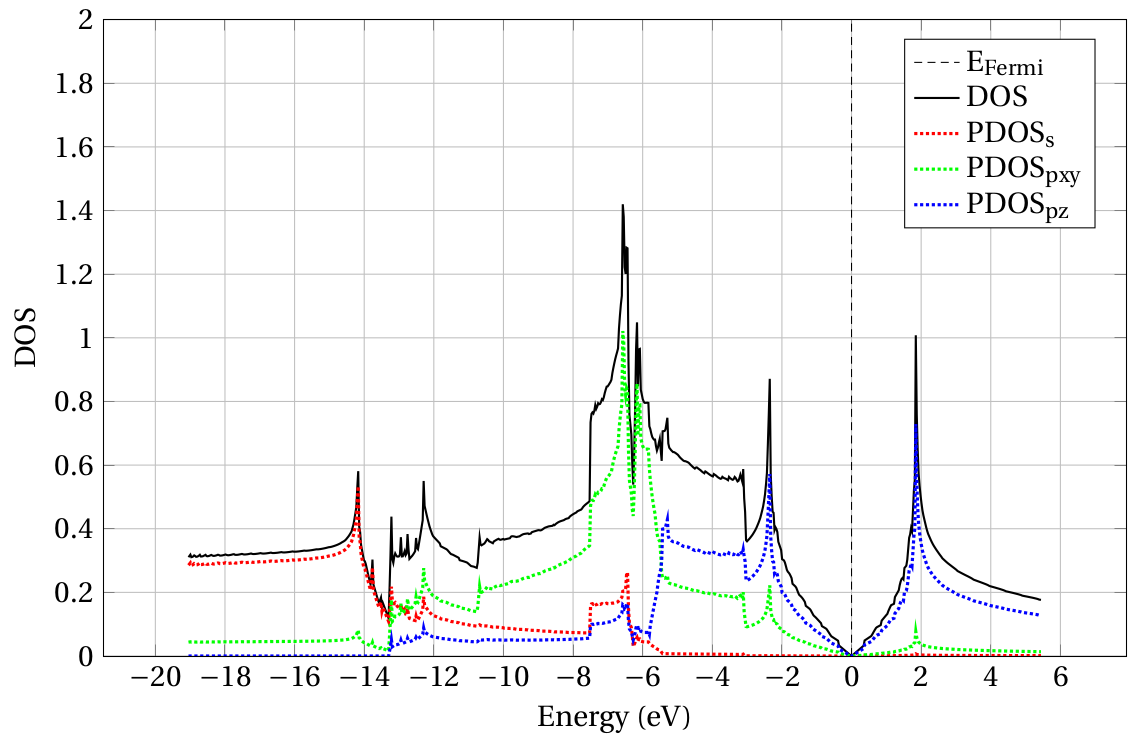
Fig. 2.4.2 Projected density of states of graphene.