2.2. Band structure calculation
Now that I obtained the ground-state density, I perform a band-structure
calculation to get an idea of the energy spectrum of graphene as a
function of k-point. Copy the following input file and save it to a text
file named c2_bs.txt.
info.calculationType = 'band-structure'
info.savepath = 'results/c2_bs'
atom.element = [1 1]
la = 4.648725932
atom.xyz = [1 1/sqrt(3) 0;1 -1/sqrt(3) 0]/2*la
domain.latvec = [1/2 sqrt(3)/2 0; 1/2 -sqrt(3)/2 0; 0 0 4]*la
domain.lowres = 0.3
element.species = 'C'
element.path = './C_TM_LDA.mat'
kpoint.sympoints = {'G','M','K','G'}
LCAO.status = 1
rho.in = 'results/c2_scf'
Then pass it to RESCU and execute the program as follows
rescu -i c2_bs.txt;
New keywords are highlighted in blue. I will briefly explain each modification and addition.
info.calculationTypetells RESCU to perform a band-structure calculation;info.savepathwas changed not to overwrite the self-consistent results;kpoint.sympointsis a list of strings referring to edges of the irreducible Brillouin zone. The list may also contain direct coordinates along with strings. Definitions for various lattice types can be found in the Band Structure section of the User Manual;rho.inis a string pointing to the file containing the self-consistent results.
The resulting band structure is found in Fig. 2.2.1. The top of the valence band and the bottom of the conduction band overlap at a single point: \(K=[1/3\;1/3\;0]\). A neighbourhood of this point is often referred to as a Dirac cone because the energy has a linear dispersion with respect to k-point.
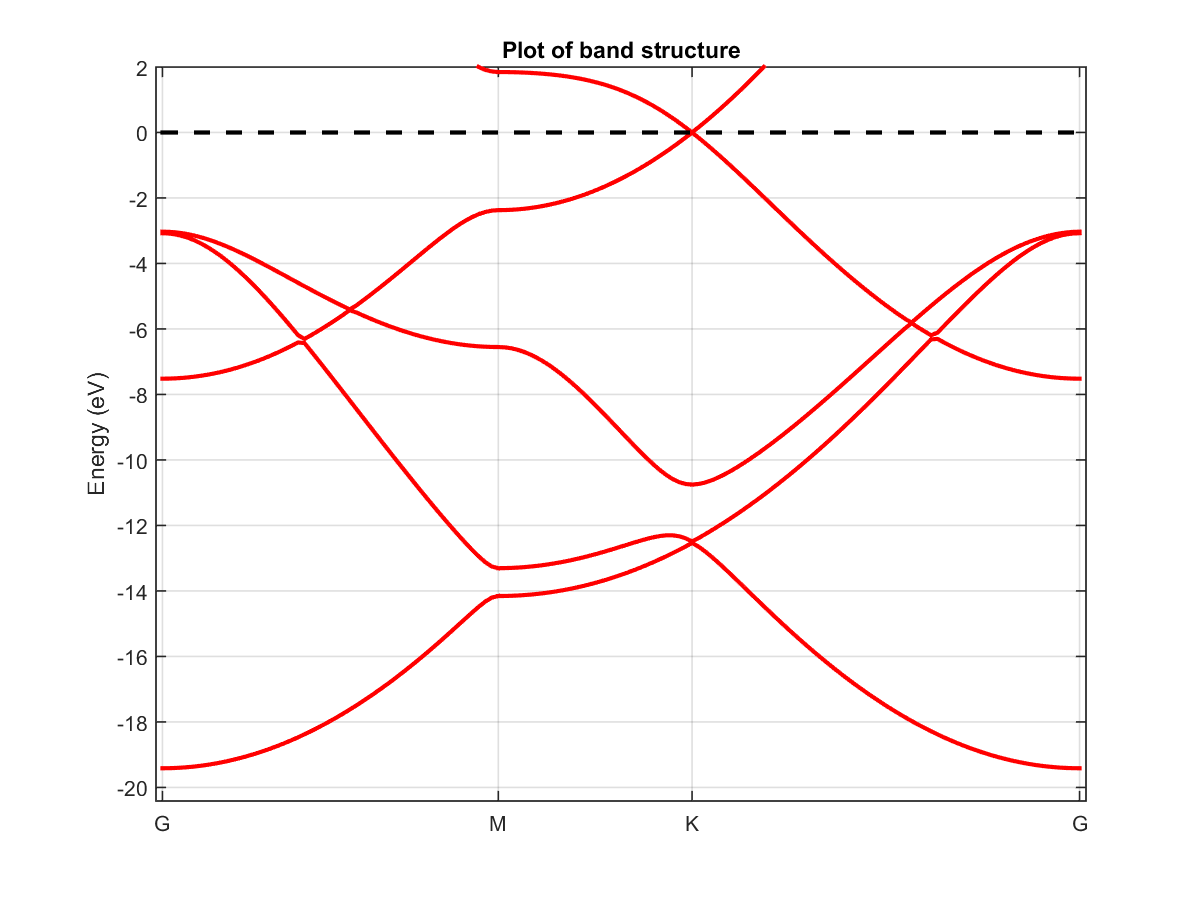
Fig. 2.2.1 Band structure of graphene.