2.3. Density of states calculation
In the present section, I compute the density of states (DOS) of
graphene. To do so, I set the keyword dos.status equal to true in
the self-consistent calculation input file. I plot the density of states
by calling RESCU with the plot option followed by the path to the
results.
rescu -p results/c2_scf.mat
The DOS is shown in Fig. 2.3.1 as a pale red
dashed line. RESCU computes the DOS in the interval
[\(E_{Fermi}\) -10, \(E_{Fermi}\)+10] eV using a resolution of
10\(^{-3}\) Bohr (0.027 eV) by default. The DOS looks like a
piecewise linear function. This is an artefact of the tetrahedron method
arising because of insufficient k-point sampling. Obtaining an accurate
DOS does not require additional k-sampling during the self-consistent
cycle, but it does require additional k-sampling for the DOS
calculation. I thus calculate non-self-consistently the spectrum of the
Kohn-Sham Hamiltonian to obtain the DOS of graphene. Copy the following
input file and save it to a text file named c2_dos.txt.
info.calculationType = 'dos'
info.savepath = 'results/c2_dos'
atom.element = [1 1]
la = 4.648725932
atom.xyz = [1 1/sqrt(3) 0;1 -1/sqrt(3) 0]/2*la
domain.latvec = [1/2 sqrt(3)/2 0; 1/2 -sqrt(3)/2 0; 0 0 4]*la
domain.lowres = 0.3
dos.range = [-0.70,0.20]
element.species = 'C'
element.path = './C_TM_LDA.mat'
kpoint.gridn = [60,60,1]
kpoint.shift = [0,0,0]
LCAO.status = 1
rho.in = 'results/c2_scf'
Then pass it to RESCU and execute the program as follows
rescu -i c2_dos.txt;
New keywords are highlighted in blue. I will briefly explain each of them.
info.calculationTypetells RESCU to perform a dos calculation;info.savepathwas changed not to overwrite the self-consistent results;dos.rangedefines the energy interval for which the DOS is calculated. As mentioned earlier, the units are in Hartree. We concentrate on the interval [-20,5] eV relative to the Fermi level in the present example;kpoint.gridnthe k-point grid was augmented to a \(60\times60\) points grid;kpoint.shiftuse a \(\Gamma\)-centred grid. RESCU uses a MonkHorst-Pack grid by default such that the default shift is \([1/2\;1/2\;1/2]\) for an even-numbered grid. A \(\Gamma\)-centred grid is necessary because we need a k-point at \(K=[1/3\;1/3\;0]\) and the number of irreducible k-points is much smaller this way.
I plot the DOS using the following command.
rescu -p results/c2_dos.mat
The result is shown in Fig. 2.3.1 as a solid red line. The overall shape is compatible with the self-consistent result, but specific features are now resolved much more accurately.
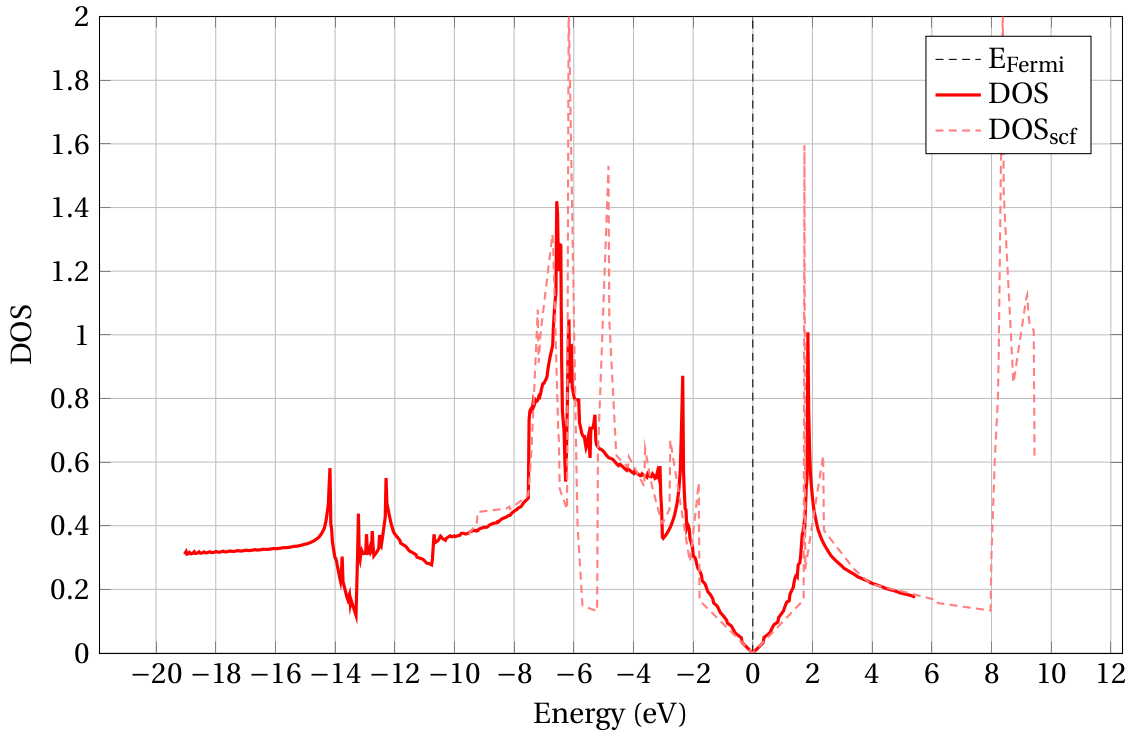
Fig. 2.3.1 Density of states of graphene.