5. Multivalley effective-mass theory solver
Envelope-function approximation
We consider a material with conduction-band minima (valleys) located at \(\mathbf k_\nu\) (\(\nu\) being the valley index) under the influence of a confinement potential, \(V_{\mathrm{conf}}(\mathbf r)\). Under effective-mass theory and the envelope function approximation, we approximate the conduction-electron wavefunctions as [GJN+15, SN76]
In Eq. (5.1), we have introduced \(F_\nu(\mathbf r)\), the envelope function for valley \(\nu\), and \(\xi_\nu(\mathbf r)\equiv u_\nu(\mathbf r)\mathrm e^{i\mathbf k_\nu\cdot\mathbf r}\), the Bloch function evaluated at the \(\nu\)-th conduction band minimum, with \(u_\nu (\mathbf r)\) being the lattice-periodic Bloch amplitude of this state.
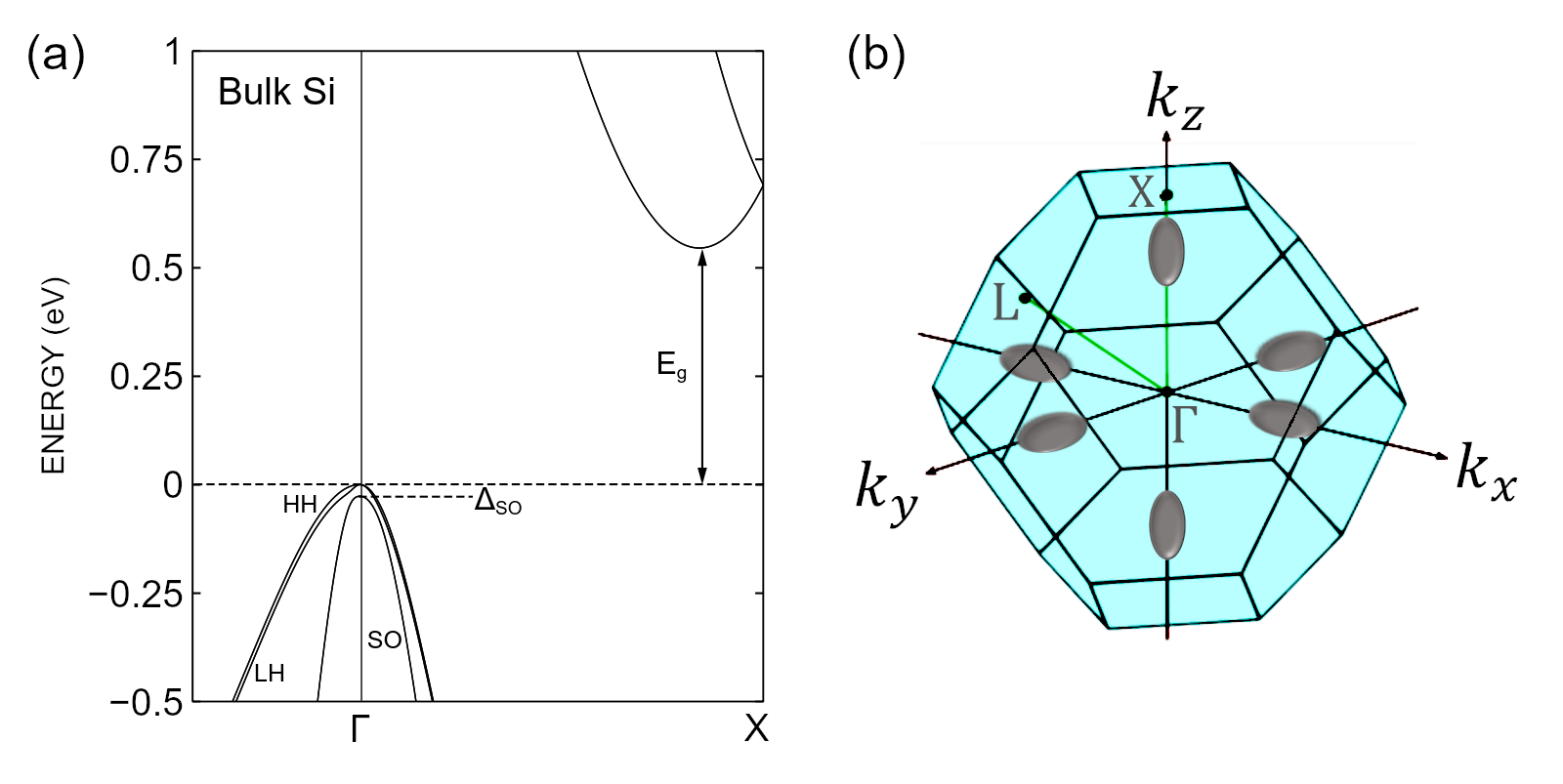
Fig. 5.1 Degenerate conduction-band minima (valleys) in silicon. (a) Band structure of silicon (Si). (b) First Brillouin zone of silicon. The ellipsoids are equipotential surfaces of the conduction band of silicon near its six equivalent minima located away from the \(\Gamma\) point along the \(\pm \mathbf{\hat x}\), \(\pm \mathbf{\hat y}\), and \(\pm \mathbf{\hat z}\) directions, at roughly 85 % of the distance between the \(\Gamma\) point and the zone boundary (only the X point is shown above). The band structure in (a) was calculated using Nanoacademic’s atomistic simulation software NanoDCAL (see, e.g., the NanoDCAL tutorial on Spin–orbit interaction). Similar calculations can also be done with RESCU and RESCU+. The band structure was calculated using the local density approximation (LDA), which correctly predicts numerous properties of crystals but underestimates band gaps.
Under the envelope-function approximation, it is assumed that the confinement potential, \(V_{\mathrm{conf}}(\mathbf r)\) and the envelope functions, \(F_\nu(\mathbf r)\), vary negligibly over a lattice spacing. In other words, it is assumed that \(V_{\mathrm{conf}}(\mathbf r)\) and \(F_\nu(\mathbf r)\) have Fourier components, \(\mathbf{q}\), with significant weight only if \(q \ll 1/a\), where \(a\) is the lattice constant. Accordingly, a slowly-varying \(V_{\mathrm{conf}}(\mathbf r)\) cannot couple Bloch waves separated by large distances relative to the size of the Brillouin zone. Because we are typically interested in materials with valleys separated by large distances in reciprocal space (e.g., silicon), we can write a set of uncoupled differential equations for each envelope function, \(F_\nu(\mathbf r)\)
where \(\mathbf M_\nu^{-1}\) is the effective mass tensor for valley
\(\nu\).
Under the envelope function approximation, there is therefore an effective-mass
equation [equivalent to Eq. (3.1)] for each
valley.
These equations can be solved by the Schrödinger
Solver in
QTCAD and the theory is equivalent to that presented in
Effective Schrödinger equation for electrons.
MVEMT Differential equations
In certain (common) structures (e.g., at a heterointerface or at the location of a dopant), the confinement potential, \(V_{\mathrm{conf}}(\mathbf r)\), varies significantly over the lattice spacing. Accurately modeling these structures requires going beyond the envelope-function approximation to account for the coupling between valleys. One way to approach this problem is to solve the multi-valley effective-mass theory (MVEMT) equations [GHCJ+16, GJN+15]
Note that while there is still one equation for each valley, in contrast to (5.2), these equations are coupled by the term \(V^\mathrm{VO}_{\nu\nu'}(\mathbf r)\) which can be expressed in terms of the confinement potential, \(V_{\mathrm{conf}}(\mathbf r)\), as
The coupled differential equations in Eq. (5.3) can be reexpressed in matrix form as
where \(\mathbf{K}\) is the kinetic energy matrix with matrix elements \(\mathbf{K}_{\nu\nu'} = \frac{\hbar^2}{2}\mathbf{k}\cdot\mathbf M^{-1}_\nu\cdot \mathbf{k}\;\delta_{\nu\nu'}\), \(\mathbf{V}^\mathrm{VO}\) is the valley–orbit coupling matrix with matrix elements \(\mathbf{V}^\mathrm{VO}_{\nu\nu'}(\mathbf r)\), and \(\vec{F}(\mathbf r)\) is a column vector with components \(F_{\nu}(\mathbf r)\) [this matrix equation is the equivalent of the Luttinger–Kohn matrix equation, Eq. (3.6) which is used to model holes including heavy-hole light-hole mixing]. For example, when considering the six-dimensional subspace spanned by the \(\{+x,-x,+y,-y,+z,-z\}\) valley states of silicon, we can write
To calculate the valley–orbit coupling term defined in Eq. (5.4), it is useful to write the Bloch amplitudes as a Fourier decomposition:
where \(A_\mathbf G^\nu\) is the Fourier component of the Bloch amplitude
associated with the reciprocal lattice vector \(\mathbf G\). These
Fourier components may be calculated using density-functional theory (e.g.,
with RESCU+).
In QTCAD, it is possible
to import the Fourier components of Bloch amplitudes from text files.
In particular, it is possible to import
Fourier components of the silicon Bloch amplitudes calculated in
[SCalderonC+11]; these Fourier components are stored in
qtcad/device/valleycoupling/bloch/silicon.
The coupled differential equations in Eq. (5.3) can be solved using
the MVEMT Solver in QTCAD.
More practical information on how to use this solver and the bloch_tools module may be found
in the Valley splitting (MVEMT) tutorial.
Relevant device attributes
Parameter |
Symbol |
QTCAD name |
Unit |
Default |
Setter |
Confinement potential |
\(V\) |
|
J |
0 |
|
External conf. potential |
\(V_\mathrm{ext}\) |
|
J |
0 |
Note
The total confinement potential \(V_\mathrm{conf} (\mathbf r)\) employed by the multivalley effective mass theory solver is given by \(V_\mathrm{conf} (\mathbf r) = V(\mathbf r)+V_\mathrm{ext}(\mathbf r)\).
Boundary conditions
The boundary conditions for the multi-valley effective mass theory solver are the same as for the regular Schrödinger solvers. These boundary conditions are described in Boundary conditions.