8. DFT+U
In this section, we introduce DFT+U calculations. Note that the Hubbard operator is expressed in terms of atomic orbitals, and hence even grid-based calculations ultimately depend on the quality of the NAO basis. Moreover, the use of symmetry is prohibited.
8.1. Example: DOS of nickel oxide
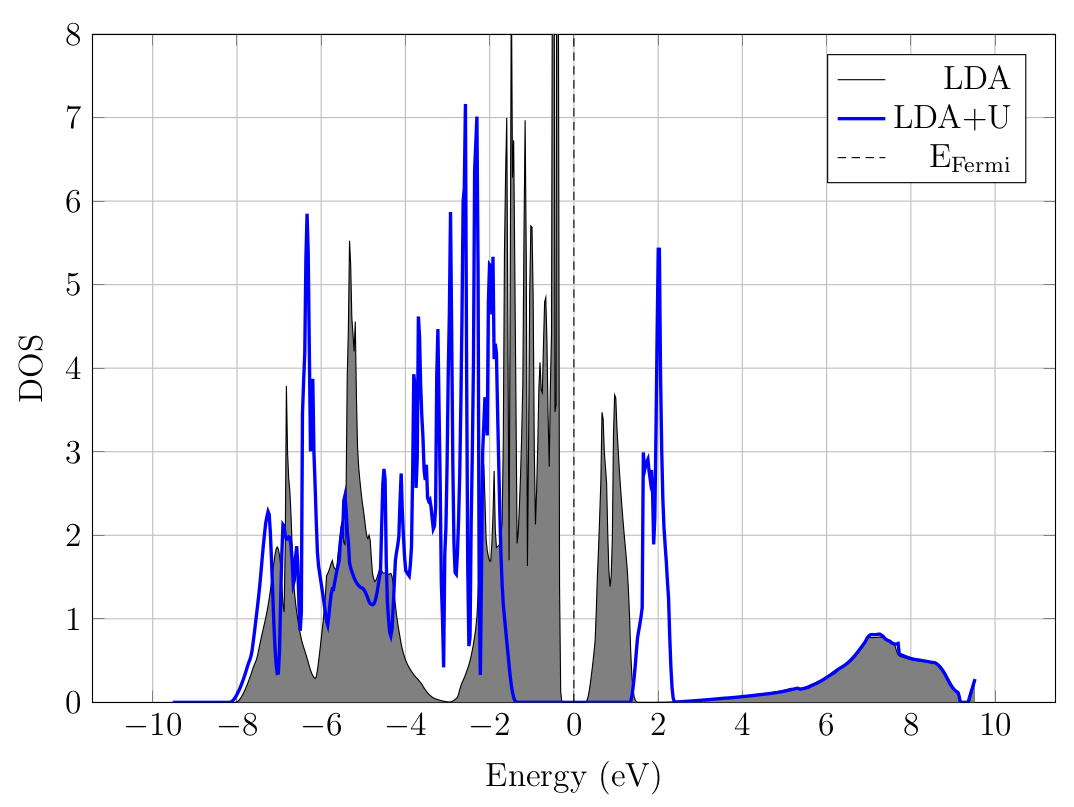
Fig. 8.1.1 DOS of nickel oxide.
In this example, we calculate the electronic structure of nickel oxide
using LDA+U. DFT+U calculations are usually more difficult to converge
than DFT calculations. As such, it is profitable to perform a DFT
calculation first and then use the results as an initial guess for the
DFT+U calculation. Name the following input file nio_lcao_scf.input
LCAO.status = true
info.savepath = 'results/nio_lcao_scf'
info.calculationType = 'self-consistent'
atom.fracxyz = 'nio_111.xyz'
domain.latvec = 4.1705*[1 0.5 0.5;0.5 1 0.5;0.5 0.5 1]; units.domain.latvec = 'a'
domain.lowres = 0.3
element(1).species = 'Ni'
element(1).path = './Ni_TM_LDA.mat'
element(1).ortho = [0 0 0 1 1]
element(2).species = 'O'
element(2).path = './O_TM_LDA.mat'
functional.libxc = 0
functional.list = {'XC_LDA_X','XC_LDA_C_PW'}
kpoint.gridn = [6,6,6]; kpoint.shift = 0.5*[1,1,1]
kpoint.sampling = 'tetrahedron+blochl'
symmetry.spacesymmetry = false
symmetry.pointsymmetry = false
symmetry.timereversal = false
spin.type = 'collinear'
option.saveDensityMatrixK = true
where the file nio_111.xyz is
4
AtomType X Y Z magmom
Ni +0.00e+00 +0.00e+00 +0.00e+00 +1.0e+00
O +2.50e-01 +2.50e-01 +2.50e-01 +0.0e+00
Ni +5.00e-01 +5.00e-01 +5.00e-01 -1.0e+00
O +7.50e-01 +7.50e-01 +7.50e-01 +0.0e+00
Nickel oxide is arranged in a rock salt lattice, but its
anti-ferromagnetic ground state breaks the atomic ordering. We thus use
a rhombohedral supercell containing four atoms, and initialize the
magnetic ordering using the fifth column of the xyz file
nio_111.xyz. As usual, let’s make a few comments about the keywords
used in the input file.
atom.fracxyzpoints to the xyz file containing the fractional atomic coordinates.element.orthospecifies atomic orbitals to be orthonormalized. In DFT+U calculations, the atomic orbitals with a nonzero U are orthonormalized, and hence the same orbitals should be orthonormalized in the regular DFT calculation to yield a compatible density matrix.kpoint.shiftis used to shift the k-point grid. Since even Monkhorst-Pack grids are shifted away from \(\Gamma\), the shift of 0.5 brings the grid back on \(\Gamma\).spin.typedetermines how spin is treated. Here we use the collinear spin formulation of DFT because nickel oxide is anti-ferromagnetic.option.saveDensityMatrixKtells RESCU to save the density matrix calculated at every k-point. This way, it can be reused as an initial guess in the DFT+U calculation.
You may then run RESCU as follows
rescu -i nio_lcao_scf.input
Next comes the DFT+U calculation. Define the file
nio_lcao_scf_u.input as follows
LCAO.status = true
info.savepath = 'results/nio_lcao_scf_u'
info.calculationType = 'self-consistent'
atom.fracxyz = 'nio_111.xyz'
domain.latvec = 4.1705*[1 0.5 0.5;0.5 1 0.5;0.5 0.5 1]; units.domain.latvec = 'a'
domain.lowres = 0.3
element(1).species = 'Ni'
element(1).path = './Ni_TM_LDA.mat'
element(1).CoulombEnergyU = [0 0 0 4 4]; units.element.CoulombEnergyU = 'ev'
element(2).species = 'O'
element(2).path = './O_TM_LDA.mat'
functional.libxc = 0
functional.list = {'XC_LDA_X','XC_LDA_C_PW'}
functional.includeU = 1
kpoint.gridn = [6,6,6]; kpoint.shift = 0.5*[1,1,1]
kpoint.sampling = 'tetrahedron+blochl'
spin.type = 'collinear'
rho.in = 'results/nio_lcao_scf'
LCAO.DMkcell = rho.in
dos.status = true
LCAO.mulliken = true
where nio_111.xyz remains the same. The input is essentially
untouched except for the following keywords
element.CoulombEnergyUdefines the Hubbard U (in atomic units) for the atomic orbitals in the pseudopotential fileelement.path. Here, we set the U parameter of the fourth and fifth orbitals (d-orbitals) of the nickel atoms to 0.1470 Hartree (4 eV) and zero otherwise. The U parameter of the oxygen orbitals is not specified, and hence it is initialized to zero as well.functional.includeUdetermines whether to include the Hubbard term in the Hamiltonian and total energy.LCAO.DMkcelltells RESCU where the density matrix for each k-point is saved. In this example, we point to the DFT results.dos.statusis set totrueto compute the DOS at the end of the self-consistent calculation.LCAO.mullikenis set totrueto compute the Mulliken populations at the end of the self-consistent calculation.
Then execute RESCU as follows
rescu -i nio_lcao_scf_u.input
First, inspecting the results in results/nio_lcao_scf_u.h5, you
should find that the nickel atoms’ magnetic moment, as calculated using
the Mulliken populations, increased from roughly 1.2 \(\mu_B\) in
the LDA to 1.8 \(\mu_B\) in the LDA+U. Next, you may plot the DOS
typing
rescu -p results/nio_lcao_scf_u
You should get a plot similar to Fig. 8.1.1. The band gap visibly increases, from about 0.5 eV in the LDA to 2.6 eV in the LDA+U. Note that the valence DOS is modified significantly, which only the conduction band minimum is affected.