13. Linear combination of atomic orbitals (LCAO)

RESCU uses numerical atomic orbitals for various purposes. Most functions work either in a pure real space framework or in the atomic orbital framework. The computational burden is typically significantly lower using an atomic orbital basis, and hence it is often advantageous to switch between the two schemes and compare results.

13.1. Example: band structure of silicon

To perform an NAO calculation, set the keyword LCAO.status to true. This is what is done in the following example.

info.calculationType = 'self-consistent'
info.savepath = './results/si_lcao_scf';
element(1).species = 'Si';
element(1).path = './Si_TM_LDA.mat';
atom.xyz = 10.25 * ...
  [[     0         0         0]
    [0.2500    0.2500    0.2500]];
atom.element = ones(2,1);
domain.latvec = 10.25/2*[0 1 1;1 0 1;1 1 0];
domain.lowres = 0.4;
diffop.method = 'fft';
functional.list = {'XC_GGA_X_PBE','XC_GGA_C_PBE'};
kpoint.gridn = [4,4,4];
LCAO.status = true;

In most situations, there is really a single important keyword controlling the computational framework:

• switch to turn on and off the LCAO mode. When it is true, RESCU performs an NAO calculation instead of a real space calculation.

Below lies an input file to calculate a band structure from the results obtained running the script above. The plot can be found in Fig. 13.1.1. The calculation was also performed in real space for comparison. There is a good agreement between the real space results and the NAO results in an interval roughly \([-7,3]\) around the Fermi level. We note the bump at the lowest point of the valence band which is an artefact of the atomic orbitals. There is also disagreement in the higher conduction bands.

info.calculationType = 'band-structure'
info.savepath = './results/si_lcao_bs';
kpoint.sympoints = {'L','G','X','W','K'};
kpoint.gridn = 101;
rho.in = './results/si_lcao_scf';
LCAO.status = true;

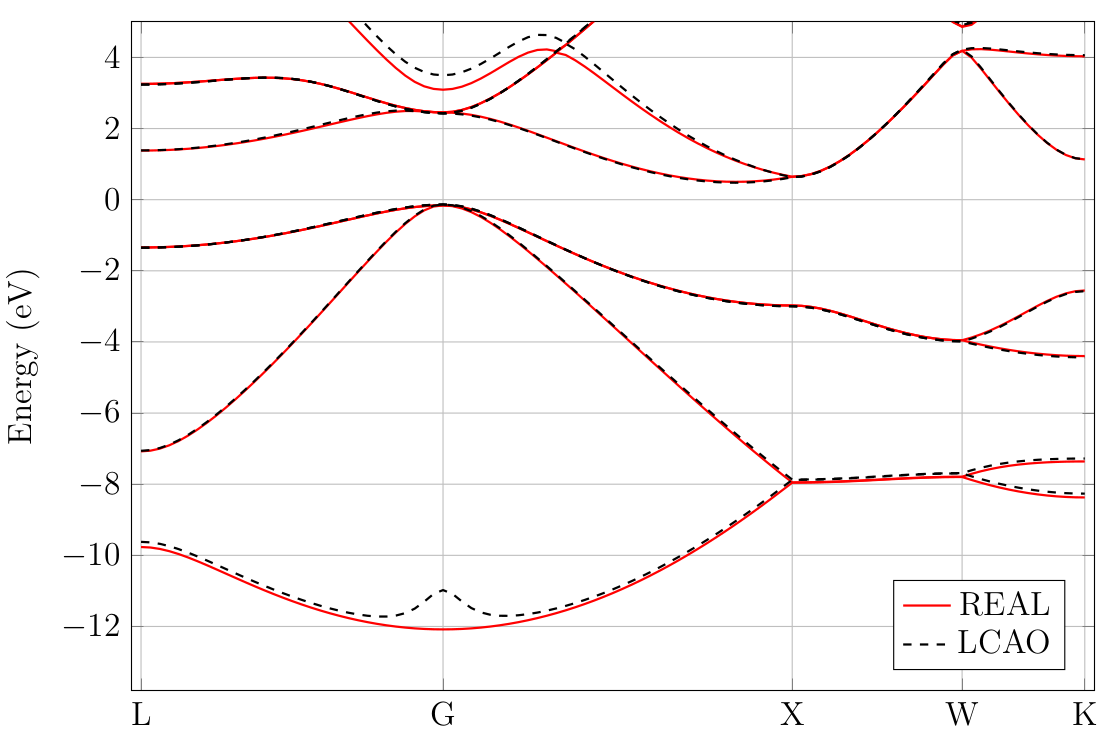
Fig. 13.1.1 Silicon band structure computed in real space and in a numerical atomic orbital basis.