5. Band unfolding calculation
In this section, we show how to unfold the band structure of Cu\(_3\)Au [PZ12].
5.1. Example: band structure of Cu\(_3\)Au
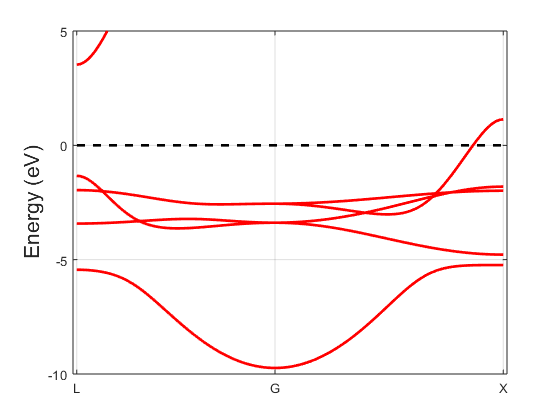
Fig. 5.1.1 Copper band structure
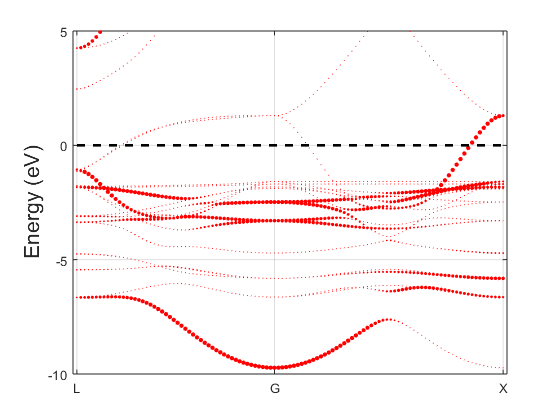
Fig. 5.1.2 Cu\(_3\)Au spectral function
The Cu\(_3\)Au crystal has a simple cubic unit cell with a gold atom at the origin and three face-centered copper atoms. Let’s obtain the ground state density using the following input file
LCAO.status = 1
info.calculationType = 'self-consistent'
info.savepath = 'results/Cu3Au_lcao_scf'
info.outfile = 'fCu3Au_lcao_scf.out'
atom.fracxyz = 0.5*[0 0 0;0 1 1;1 0 1;1 1 0]
atom.element = [1 2 2 2]
domain.latvec = 3.74*eye(3); units.latvec = 'a'
domain.lowres = 0.250000
element(1).species = 'Au'
element(1).path = './Au_TM_LDA.mat'
element(2).species = 'Cu'
element(2).path = './Cu_TM_LDA.mat'
functional.list = {'XC_GGA_X_PBE','XC_GGA_C_PBE'}
kpoint.sampling = 'tetrahedron+blochl'
kpoint.gridn = [10 10 10]
There is nothing special here so we proceed with the self-consistent calculation.
rescu -i Cu3Au_lcao_scf
We now turn to the band unfolding input.
info.calculationType = 'band-unfolding'
info.savepath = 'results/Cu3Au_lcao_bs_unfold'
info.outfile = 'fCu3Au_lcao_bs_unfold.out'
rho.in = 'results/Cu3Au_lcao_scf'
domain.primLatvec = 3.74*0.5*[0,1,1;1,0,1;1,1,0]; units.length = 'a'
kpoint.sympoints = {'L','G','X'}
Two keywords are worthy of mention.
info.calculationTypeis a string determining the nature of the calculation. If it is set to band-unfolding, the eigenvalues of the Hamiltonian and the effective spectral function are calculated;domain.primLatvecdetermines the primitive cell vectors. Simply put, the supercell eigenstates are projected onto the primitive cell eigenstates. The probability amplitude squared yields the effective spectral function.
In a band-unfolding calculation, the keyword kpoint.sympoints is
attached to the primitive cell and its Brillouin zone, not the
supercell. Here, the Cu\(_3\)Au crystal may be viewed as a
copper supercell with a substitutional gold impurity, and hence we
unfold onto a face centered cubic primitive cell. You may then run RESCU
as follows
rescu -i Cu3Au_lcao_bs_unfold
Upon completion, RESCU will write the basic band structure data in
BandStructure.txt and the band unfolding data in
UnfoldedBandStructure.txt. The BandStructure.txt format is
described in Example: band structure of silicon. The unfolded format is
almost identical, but there is an additional block of data, commensurate
with the energy one, which gives the spectral function (weights) of the
band structure. Additional data is found in the band structure
stored in ./results/Cu3Au_lcao_bs_unfold.mat. In particular, the
spectral function is saved in band.specFun. RESCU’s plotting tool
allows you to have a quick look at the spectral function
rescu -p results/Cu3Au_lcao_bs_unfold
The marker size for every eigenvalue is proportional to the spectral function at that energy and k-point. There is a minimal size such that all bands remain visible. You should get a figure similar to Fig. 5.1.2; the band structure of copper is shown in Fig. 5.1.1 for comparison. The band structures are qualitatively similar, but there are visible differences, usually interpreted as hybridized states.
Voicu Popescu and Alex Zunger. Extracting e versus k - Effective band structure from supercell calculations on alloys and impurities. Physical Review B - Condensed Matter and Materials Physics 85.8 (2012), pp. 1–12.