Valence band maximum tutorial

Requirements

Software components

  • nanotools

  • RESCU+

Pseudopotentials

I will need the following pseudopotential file.

  • C_LDA_TM_DZP.mat

Let’s copy it from the pseudo database to the current working directory and export RESCUPLUS_PSEUDO=$PWD.

Briefing

In this tutorial, I show how to calculate the valence band maximum of diamond.

Code

from nanotools import Atoms, Cell, System, TotalEnergy
from nanotools.vbm import ValenceBandMaximum as VBM
a = 3.562 / 2.
cell = Cell(avec=[[0.,a,a],[a,0.,a],[a,a,0.]], resolution=0.15)
fxyz = [[0.00,0.00,0.00],[0.25,0.25,0.25]]
atoms = Atoms(fractional_positions=fxyz, formula="C(2)")
sys = System(cell=cell, atoms=atoms)
ecalc = TotalEnergy(sys)
ecalc.solver.set_stdout("resculog.out")
ecalc.solver.set_mpi_command("mpiexec -n 2")
vcalc = VBM.from_totalenergy(ecalc)
vcalc.charge_deltas = [1.e-4,0.001,0.01]
vcalc.solve()
fig = vcalc.plot_vbm()
vcalc.print_vbm()

Explanations

In this section, I show how to obtain the electronic chemical potential or valence band maximum (VBM) of diamond. This VBM is obtained with Janak’s theorem

\[\frac{d E(n_i)}{dn_i} = e_i\]

where \(n_i\) is the occupation number of the highest occupied state \(i\) with the eigenvalue \(e_i\). Here is a high level view of the calculation workflow:

  1. Create a TotalEnergy calculator and specify calculation parameters like resolution, k-sampling, tolerance, etc.

  2. Create a ValenceBandMaximum calculator.

  3. Solve the Kohn-Sham equation for a few charge states to obtain the VBM.

Total energy calculator

I first define a diamond crystal system with a lattice constant of 3.562 Ang. I then create a total energy calculator (ecalc) from this System object. For more detail on how to setup a total energy calculation, refer to total energy tutorial.

Valence band maximum calculator

I can then initialize a VBM calculator from the total energy calculator. The VBM calculator will solve Kohn-Sham equation for various charge states to compute

\[\frac{d E(n_i)}{dn_i} = e_i\]

. The derivative is calculated by finite difference, i.e. by removing a small fractional charge from the diamond unit cell.

\[e_i = \frac{E[Q=N] - E[Q=N-\delta N]}{\delta N}\]

Trying different orders of magnitudes of finite difference is good practice. A coarse difference is inaccurate due to the linearization approximation while a tiny difference is inaccurate due to numerical errors. Here, I will use \(\delta N = {.0001, .001, .01}\). I thus need to do four calculations, one for the neutral system and three for the slightly charged systems. The VBM class takes care of that for you with the following lines

vcalc = VBM.from_totalenergy(ecalc)
vcalc.charge_deltas = [1.e-4,0.001,0.01]
vcalc.solve()

The calculator will save results to nano_vbm_out.json as the solving progresses. The results can then be loaded with the class method read.
You can finally see the VBM as a function of \(\delta N\) typing

fig = vcalc.plot_vbm()

which will produce

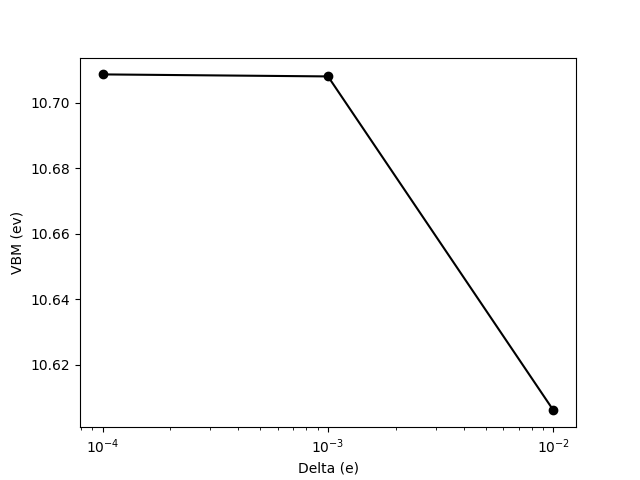
VBM as a function of delta

To check the exact VBM values, you could utilize the following method

vcalc.print_vbm()