10.8. Metals

Performing DFPT calculations for systems with zero electronic band-gap is essentially the same as calculations which are covered is previous sections, e.g. see Dynamical matrix and Born effective charges. However, there are two fundamental differences between DFPT calculations with and without electronic band-gap [G95, BGCG01]:

• Response to an electric field perturbation is not well-defined for zero band-gap systems

• Fermi energy is zero band-gap systems may vary in presence of perturbations which in turn may modify occupations of electronic states

In this section we highlight the important aspects of DFPT calculations for metals by looking at aluminum (Al) example.

We begin by simulating Al ground state using a self-consistent calculation:

info.calculationType = 'self-consistent'
info.savepath = './results/al_real_scf'
element(1).species = 'Al'
element(1).path = './Al_AtomicData.mat'
atom.element = [1]
atom.xyz = [0 0 0]
domain.latvec = 7.665*[0.5,0.5,0.0;0.0,0.5,0.5;0.5,0.0,0.5]
domain.lowres = 0.2
functional.libxc = true
functional.list = {'XC_LDA_X','XC_LDA_C_PW'}
kpoint.gridn = [5 5 5]
kpoint.sampling = 'gauss'   % required for dfpt for metals
kpoint.sigma = 0.025        % required for dfpt for metals
mixing.tol = 1e-8*[1 1]     % advised for dfpt
option.saveWavefunction = 1 % required for dfpt
diffop.method = 'fft'       % required for dfpt
domain.fourierInit = false  % required for dfpt

Unlike calculations in Dynamical matrix and Born effective charges, kpoint.sigma has a non-zero value which is used to distinguish a metallic calculation from a non-metallic one in DFPT.

Important

Non-zero value of kpoint.sigma triggers a subsequent metallic DFPT calculation. Also kpoin.sampling determines the type of smearing that is used in simulations, and current implementation of DFPT supports gauss and fermi-dirac smearings.

RESCU is executed as follows

rescu -i al_real_scf

Next, we perform a DFPT phonon calculation to compute the dynamical matrix:

info.calculationType = 'dfpt-phonon'
info.savepath = './results/al_real_phonon'
rho.in = './results/al_real_scf.mat'
psi.in = './results/al_real_scf.h5'
mixing.tol = 1e-5*[1 1]     % advised for dfpt
option.saveWavefunction = 0
symmetry.spacesymmetry = 1
symmetry.pointsymmetry = 1
symmetry.timereversal = 1

Here, there is no need to save the perturbed wavefunctions so option.saveWavefunction = 0.

rescu -i al_real_phonon

After obtaining the dynamical matrix by a self-consistent phonon calculation, we can proceed to compute full phonons band-structure and density of states. The band-structure calculation can be performed using the following input file:

info.calculationType = 'dfpt-phonon-bs'
info.savepath = './results/al_real_phonon_bs'
dfpt.phononData = './results/al_real_phonon.mat'
dfpt.qpointGridn = 96
dfpt.asr = [1,1,1]

Note

Metals do not have a well-defined dielectric constant and there is no LO-TO splitting present in their phonons band-structure.

RESCU is executed as:

rescu -i al_real_phonon_bs

The band-structure can be visualized, as in Fig. 10.8.1, using plotting option of RESCU:

rescu -p ./results/al_real_phonon_bs.mat

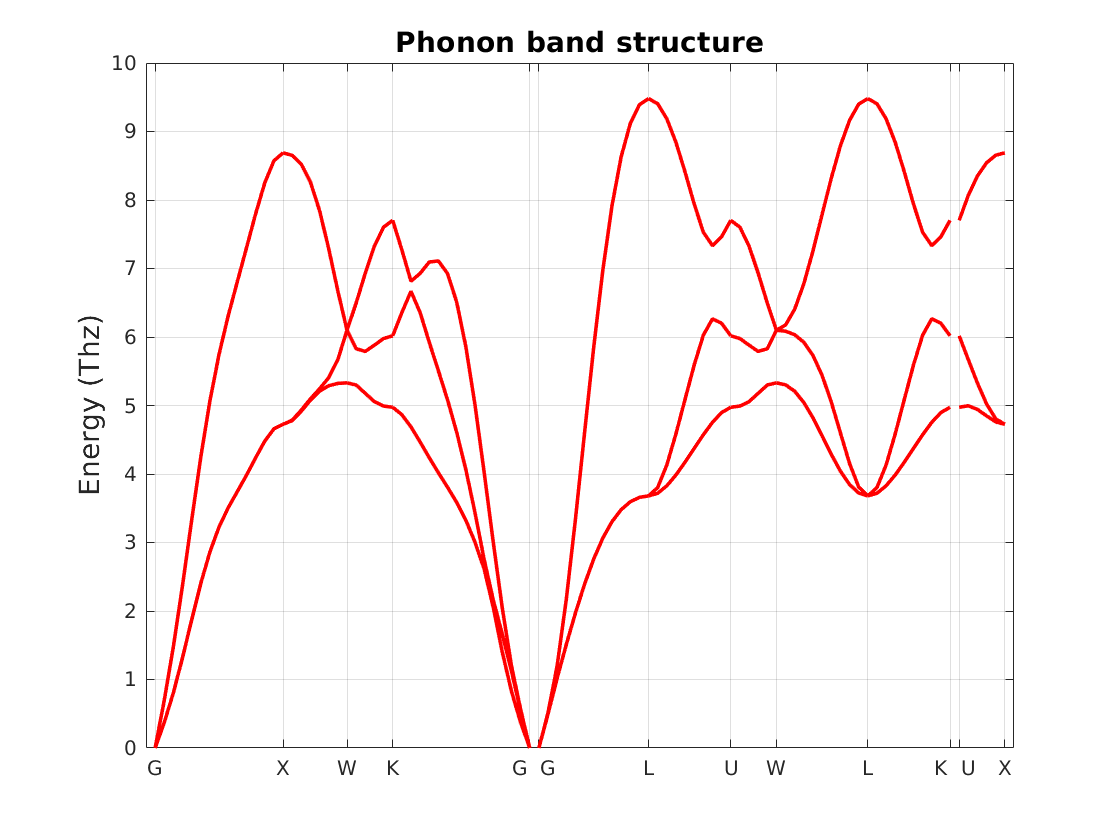
Fig. 10.8.1 Phonons band-structure of aluminum

The following input file can be used to compute phonons density of states:

info.calculationType = 'dfpt-phonon-dos'
info.savepath = './results/al_real_phonon_dos'
dfpt.phononData = './results/al_real_phonon.mat'
dfpt.qpointGridn = [10 10 10]
dfpt.asr = [1,1,1]

RESCU is executed as follows

rescu -i al_real_phonon_dos

and Al phonons DOS, Fig. 10.8.2, is plotted using:

rescu -p ./results/al_real_phonon_dos.mat

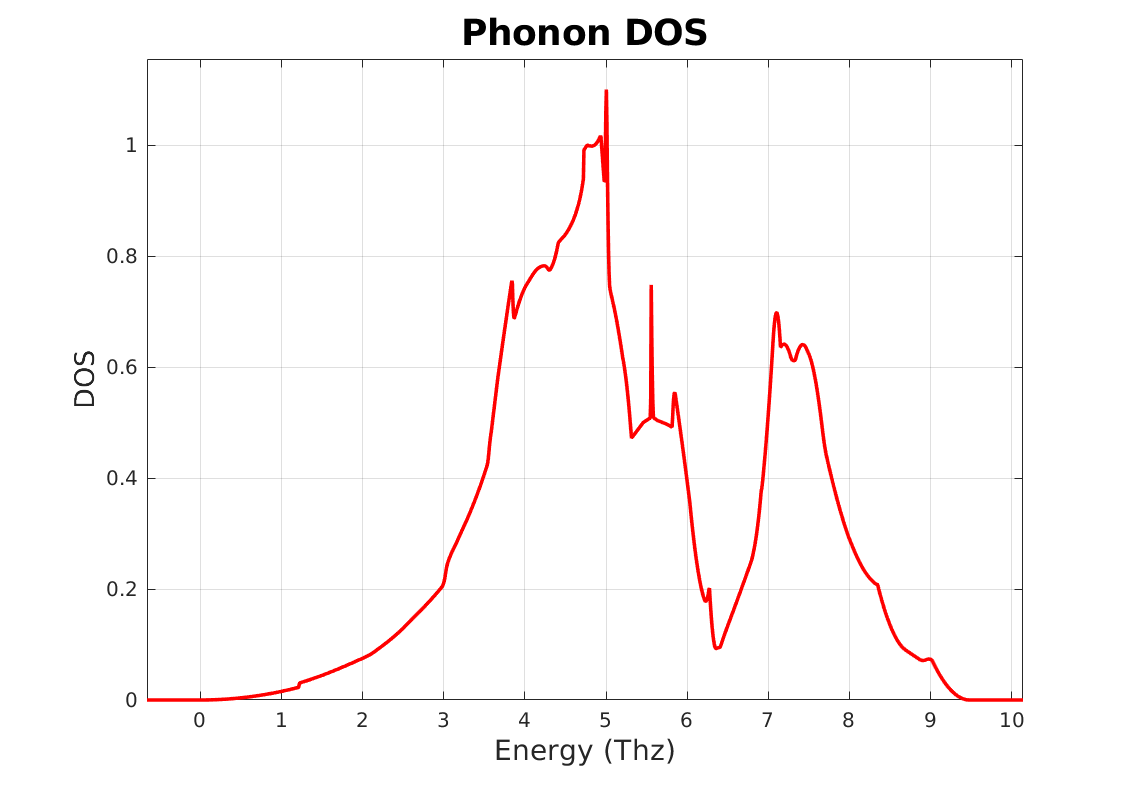
Fig. 10.8.2 Phonons DOS of aluminum

[BGCG01]

Stefano Baroni, Stefano De Gironcoli, Andrea Dal Corso, and Paolo Giannozzi. Phonons and related crystal properties from density-functional perturbation theory. Reviews of Modern Physics 73.2 (2001), p. 515.

[G95]

Stefano de Gironcoli. Lattice dynamics of metals from density-functional perturbation theory. Physical Review B 51.10 (1995), p. 6773.