10.4. Phonon band structure

In this section we use the data obtained in self-consistent phonon and dielectric DFPT calculations, to compute phonons band-structure. The band-structure is constructed by evaluating dynamical matrix eigenmodes at general \(\mathbf{q}\)-points, along high symmetry paths in brillouin zone of the crystal. Calculating the dynamical matrix at an arbitrary \(\mathbf{q}\)-points can be done in a nonself-consistent manner by using Fourier interpolation of the dynamical matrix which was obtained self-consistently by a DFPT phonon calculation [GL97]. In addition, LO-TO splitting of phonon frequencies at \(\Gamma\) can be taken into account by using the ion-clamped dielectric constant and Born effective charges.

Note

LO-TO effect is only relevant for polar materials with non-zero electronic band-gap, and is evaluated using ion-clamped dielectric constant and BECs of system.

RESCU’s input file for a phonons band-structure calculation is very similar to an electronic band-structure calculation Band structure calculation. The following example shows main keywords that control a DFPT phonons band-structure simulation:

info.calculationType = 'dfpt-phonon-bs'
info.savepath = './results/bn_real_phonon_bs'
dfpt.phononData = './results/bn_real_phonon.mat'
dfpt.dielectricData = './results/bn_real_dielectric.mat'
dfpt.qpointSympoints = {'L','G','X','W','K'}
dfpt.qpointGridn = 96
dfpt.asr = [1,1,1]

These keywords are described below.

  • info.calculationType determines the type of RESCU’s calculation;

  • info.savepath points to the file which stores the output data of the phonon band structure calculation;

  • dfpt.dielectricData points to the path of the file containing the ion-clamped dielectric tensor (only required for non-metallic systems), i.e. the output of dielectric calculation. This information is used to calculate the LO-TO corrections;

  • dfpt.phononData points to the path of the file containing the dynamical matrix and Born effective charges, i.e. the output of phonon calculation; BECs are used for calculating LO-TO corrections, and dynamical matrix is used in Fourier interplation process.

  • dfpt.qpointSympoints cell array containing the reduced coordinates or standard labels (FCC labels in the present example) of high symmetry points in brillouin zone.

  • dfpt.qpointGridn determine total number of points along the line defined by dfpt.qpointSympoints;

  • dfpt.asr it is a \(1\times 3\) vector which determines the status of various acoustic sum rules in DFPT calculations. In particular, the first two entries determines if acoustic sum rule and charge neutrality will be enforced to dynamical matrix and Born effective charges, respectively. RESCU assumes that all sum rules are active by default.

Note

Dynamical matrix and Born effective charges should fullfil certain sum rules arising from spatial invariance and total charge neutrality of the system. However, these sum rules might be slightly violated in simulations due to insufficient numerical accuracy. One can restore these sum rules by using dfpt.asr keywrod.

RESCU is executed as follows

rescu -i bn_real_phonon_bs

Nonself-consistent simulations are often faster that self-consistent ones by order of magnitudes. Upon completion, RESCU will write the band structure data in dfpt and band structures of ./results/bn_real_phonon_bs.mat output file.

>> load results/bn_real_phonon_bs.mat
>> dfpt

dfpt =

   struct with fields:

             IFC: [6x6x27 double]
             asr: [1 1 1]
            desc: [1x1 struct]
          dynMat: [6x6x98 double]
      phononFreq: [6x98 double]
      phononMode: {98x1 cell}
    qpointDirect: [98x3 double]
     qpointGridn: 96
            type: 'phonon-bs'

>> band

band =

   struct with fields:

       desc: [1x1 struct]
    kdirect: [96x3 double]
      ksnrg: [96x6 double]
   symindex: [1 31 32 67 84 96]
   symlabel: {'L'  'G'  'G'  'X'  'W'  'K'}

  • dfpt.IFC holds interatomic-force-constants data as a \(3N_{atom}\times 3N_{atom}\times N_{q}\) array.

  • dfpt.dynMat holds dynamical matrix data as a \(3N_{atom}\times 3N_{atom}\times N_{q}\). Note that q-points correspond to the points used in band-structure calculation, and not the one used in DFPT phonon calculation.

  • phononFreq holds phonon frequencies data in “THz” as a \(3N_{atom}\times N_{q}\) array.

  • phononMode holds phonon normal displacement vectors (eigenvectors) as \(N_{q}\) cell array, where each cell element is a \(3N_{atom}\times 3N_{atom}\) matrix representing the eigenvectors for corresponding q-point.

>> dfpt.phononFreq(:,1)

ans =

   15.2563
   15.2587
   27.3810
   27.6504
   27.6514
   34.4336

>> dfpt.phononMode{2}

ans =

  Columns 1 through 4

   0.0036 + 0.0005i  -0.0006 - 0.0001i  -0.0023 - 0.0005i   0.0044 + 0.0007i
  -0.0013 - 0.0002i   0.0034 + 0.0005i  -0.0022 - 0.0005i  -0.0017 - 0.0002i
  -0.0023 - 0.0003i  -0.0028 - 0.0004i  -0.0022 - 0.0005i  -0.0028 - 0.0004i
  -0.0039 + 0.0000i   0.0006 - 0.0000i   0.0030 + 0.0000i   0.0032 + 0.0000i
   0.0014 - 0.0000i  -0.0037 + 0.0000i   0.0030 - 0.0000i  -0.0012 - 0.0000i
   0.0025 + 0.0000i   0.0031 + 0.0000i   0.0030 + 0.0000i  -0.0020 + 0.0000i

  Columns 5 through 6

  -0.0006 - 0.0001i  -0.0033 - 0.0008i
   0.0041 + 0.0006i  -0.0033 - 0.0008i
  -0.0035 - 0.0005i  -0.0033 - 0.0008i
  -0.0004 - 0.0000i  -0.0020 + 0.0000i
   0.0030 + 0.0000i  -0.0020 - 0.0000i
  -0.0025 + 0.0000i  -0.0020 + 0.0000i

RESCU also writes the basic band structure data in BandStructure.txt in “Hartree”, and details of normal modes including eigenvectors in PhononBandStructure.yaml.

Phonons band-structure data stored in ./results/bn_real_phonon_bs.mat can be visualized using RESCU’s automated plotting tool to examine the quality of the calculation. Visualization is performed by executing the following command

rescu -p ./results/bn_real_phonon_bs.mat

RESCU displays a plot of band structure which is also saved to bn_real_phonon_bs_plot.fig.

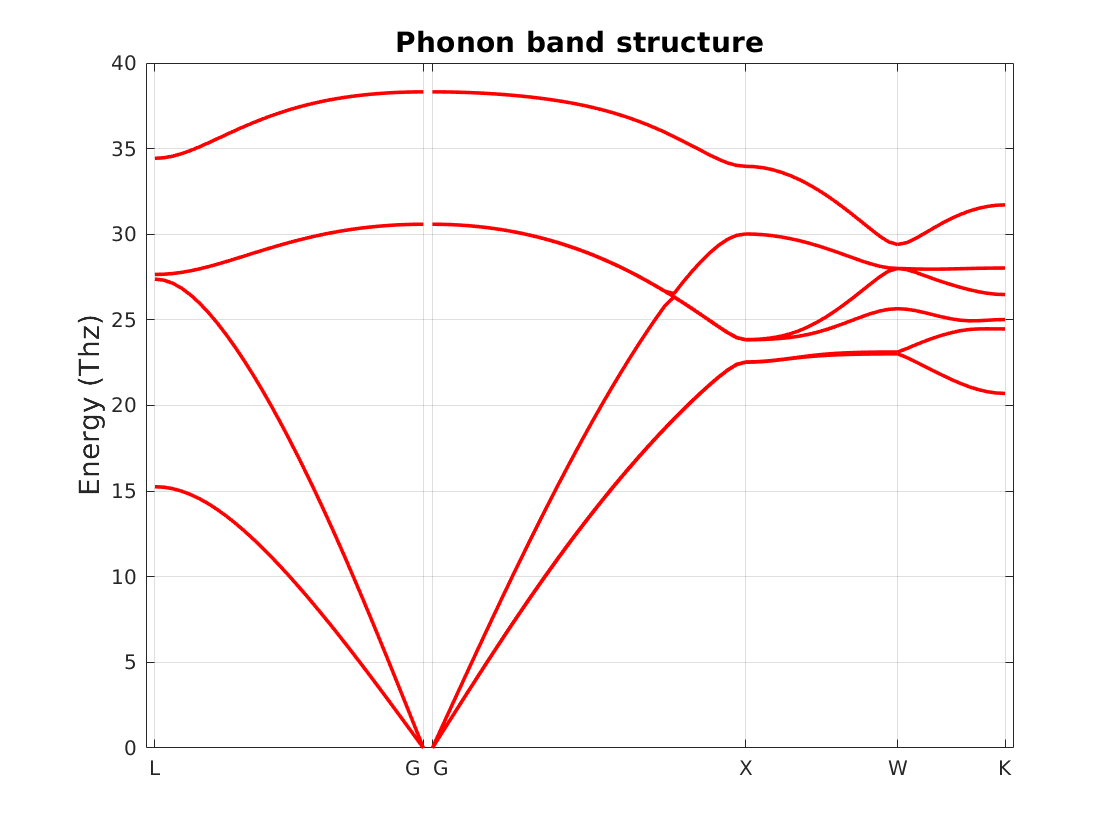
Boron nitride phonon band structure

Fig. 10.4.1 Boron nitride phonon band structure