4.5. Band structure decomposition

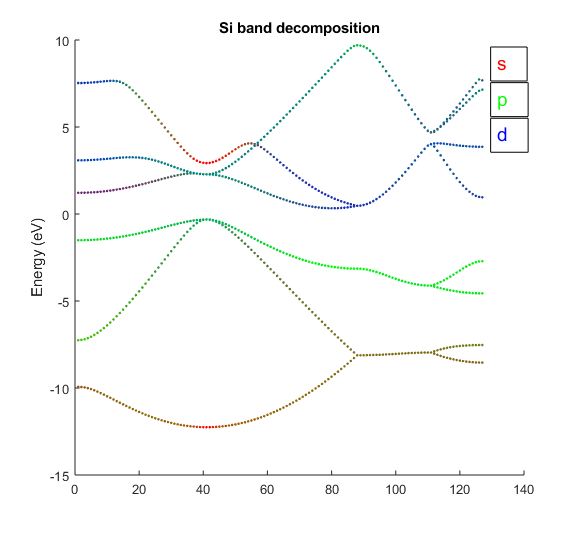
Fig. 4.5.1 Silicon band structure colored according to their \(s\), \(p\), \(d\) character.

Band structure decomposition is a useful tool to analyze a system’s spectrum, whereby each eigenstate is decomposed into atomic orbital components, giving rise to as many partial weights as there are atomic orbitals. One may then know, for example, if a band is more strongly \(s\) or \(p_z\) in character. The band decomposition can be calculated and saved by setting the keyword option.savePartialWeights to true. Define the input file si_real_bs_pw as follows

info.calculationType = 'band-structure'
info.savepath = './results/si_real_bs_pw';
kpoint.type = 'line';
kpoint.gridn = 32;
kpoint.sympoints = {'L','G','X','W','K'};
rho.in = './results/si_real_scf';
option.savePartialWeights = true

and pass it to RESCU

rescu -i si_real_bs_pw

The partial weights for every band, k-point and spin are stored in the HDF5 file ./results/si_real_bs_pw.h5. They can be loaded as follows

h5path = './results/si_real_bs_pw.h5';
wii = loadDistArray(h5path,'/LCAO/partialWeight1');

where wii is a \(n_{nao}\times n_{bnd}\) matrix. The orbital information for each row is stored in LCAO.orbInfo in ./results/si_real_bs_pw.mat. If the data is not too large, it will also be saved to a text file named DecomposedBandStructure.txt. The format is the same as that of BandStructure.txt, but there are additional blocks containing the atomic orbital weights. For each k-point and spin degrees of freedom, one will find the \(n_{nao}\times n_{bnd}\) matrix of partial weights. The order is as follows \({k_1^1,...,k_{n_k}^1,k_1^2,...,k_{n_k}^{n_s}}\); the k-points come in order and there are two sets of blocks if spin is included. In Fig. 4.5.1, the color of each marker is defined using RGB proportional to the \(s\)-, \(p\)- and \(d\)-orbital character respectively. Such figures can be generated using a script such as examples/weightedBS. Note that the partial weights may be negative because the atomic orbital basis is generally not orthogonal, and the sum of the weights may not be equal to one since the atomic orbital basis is not complete (unless the calculation was performed from LCAO).