9.3. Example: LDOS of graphene

In this section, we show how to calculate a real space representation of the DOS: the local density of states. LDOS calculations are quite similar to DOS calculations, only that at the end, the density is calculated only from states lying at a specific energy. Again, assuming that the self-consistent ground state density of graphene may be found in ./results/gr_lcao_scf.h5 and ./results/gr_lcao_scf.mat, one may compute the LDOS of graphene using the following input script

info.calculationType = 'dos'
info.savepath = 'results/gr_lcao_ldos'
kpoint.sampling = 'tetrahedron'
kpoint.gridn = [45,45,1]
rho.in = 'results/gr_lcao_scf'
dos.ldos = true

We simply set the keyword dos.ldos equal to true. Let’s introduce a few keywords providing additional control on the LDOS.

  • dos.ldos determines whether to calculate the local density of states.

  • dos.ldosEnergy contains the energies at which the local density of states is calculated.

  • dos.ldosERange the LDOS will be calculated including all states within the range of energies given by dos.ldosERange (9.3.1). Notice that setting the value to \([-\infty,\epsilon_F]\) yields the ground state density.

  • dos.ldosShiftEf if true, the LDOS energies are relative to the Fermi energy.

(9.3.1)\[\rho^{[\epsilon_1,\epsilon_2]}(\mathbf{r}) = \int\limits_{\epsilon_1}^{\epsilon_2} d\epsilon \rho(\mathbf{r},\epsilon)\]

Note that the LDOS energies specified by dos.ldosEnergy or dos.ldosERange are absolute unless the keyword dos.ldosShiftEf is set to true. In the previous example, only dos.ldos is specified, and hence the LDOS is calculated at the Fermi energy. The LDOS is saved in the /dos/ldosVal data set of ./results/gr_lcao_ldos.h5. This is visible typing

h5disp('results/gr_lcao_ldos.h5')
Group '/dos'
Dataset 'ldosVal'
Size:  17152x1
MaxSize:  17152x1
Datatype:   H5T_IEEE_F64LE (double)
ChunkSize:  []
Filters:  none
FillValue:  0.000000
Attributes:
'real':  1.000000

As we have seen in the previous section, we expect the DOS to have \(p_z\) character there. This is indeed apparent in Fig. 9.3.1 which shows an isosurface of the LDOS.

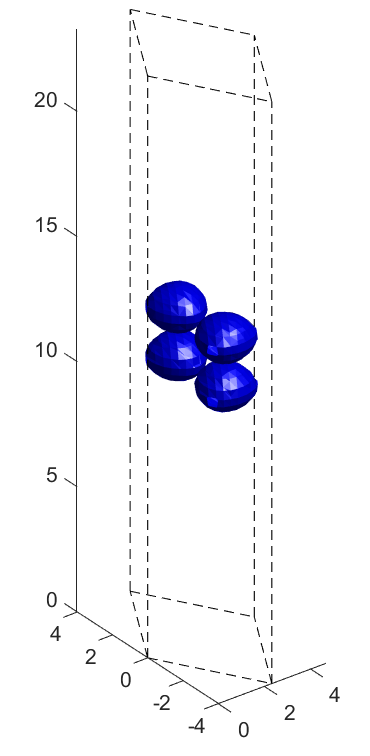
LDOS of graphene at the Fermi level.

Fig. 9.3.1 LDOS of graphene at the Fermi level.

The projected LDOS (PLDOS) may also be calculated using the same keywords as the projected DOS (see section 1.2). For instance, you could set dos.projAtom = 1 in the above example and you’d see a single \(p_z\) orbital instead of the two in Fig. 9.3.1. The PLDOS are saved in the /dos/pldosVal data set of ./results/gr_lcao_ldos.h5.