6. Band alignment in heterostructures

6.1. Requirements

6.1.1. Software components

• QTCAD

• Gmsh

6.1.2. Geometry file

• qtcad/examples/tutorials/meshes/band_alignment.geo

6.1.3. Python script

• qtcad/examples/tutorials/band_alignment.py

6.1.4. References

• Band alignment in heterostructures

• Schrödinger solvers

6.2. Briefing

In this tutorial, we give an example of a 1D GaAs/AlGaAs and show how multiple approaches influence band alignment. We also give examples of free and bound states obtained from the Schrödinger solver.

The full code may be found at the bottom of this page, or in qtcad/examples/tutorials/band_alignment.py.

For more information on band alignment, please read the Band alignment in heterostructures section of this documentation.

6.3. Mesh generation

As usual, the mesh is generated from the geometry file by running Gmsh with

gmsh examples/tutorials/meshes/band_alignment.geo

In the Gmsh GUI, clicking Options > Geometry, we may modify the GUI parameters to show the physical lines corresponding to each region of the device.

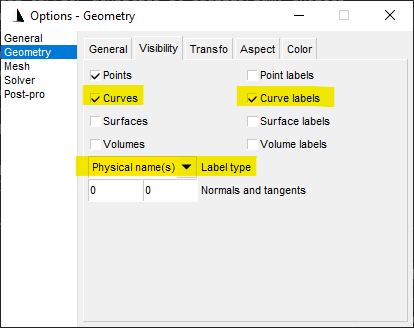
Fig. 6.3.1 Options in Gmsh visualization.

This results in

Fig. 6.3.2 1D mesh

The left_barrier and right_barrier regions will be AlGaAs, and the well region will be GaAs, thus forming a 1D rectangular potential well.

6.4. Setting up the device, aligning bands, and solving Schrödinger’s equation

6.4.1. Header

A header is first written to import relevant modules from the QTCAD Device simulator.

import numpy as np
from matplotlib import pyplot as plt
from pathlib import Path

from qtcad.device import constants as ct
from qtcad.device.mesh1d import Mesh
from qtcad.device import Device
from qtcad.device import materials as mt
from qtcad.device import analysis as an
from qtcad.device.schrodinger import Solver

6.4.2. Defining the mesh

The QTCAD mesh is defined by loading the mesh file produced by Gmsh and setting units of length

# Path to mesh file
path = Path(__file__).parent.resolve()
path = path / "meshes" / "band_alignment.msh"

# Load the mesh
mesh = Mesh(1e-9,path)

6.4.3. Creating the device

The device to simulate is then initialized on the mesh defined above, and materials are set for each region.

# Create the device and add materials
dvc = Device(mesh, conf_carriers="e")

dvc.new_region("left_barrier", mt.AlGaAs)
dvc.new_region("well", mt.GaAs)
dvc.new_region("right_barrier", mt.AlGaAs)

6.4.4. Anderson’s rule

As explained in the Band alignment in heterostructures section, by default, bands are aligned according to Anderson’s rule. We may view this default band alignment with

# Show the band diagram obtained from Anderson's rule
an.plot_bands(dvc, title="Anderson's rule")

and the result is

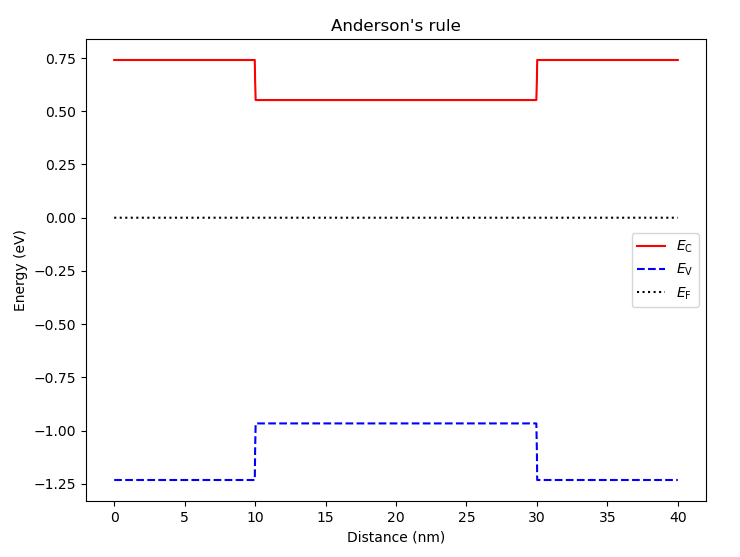
Fig. 6.4.1 Band alignment from Anderson’rule

The total confinement potential \(V_\mathrm{conf}(x)\) for electrons will be set by the conduction band edge \(E_C\).

We first visualize the default confinement potential

# View the total confinement potential before calling set_V_from_phi
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)",
   title="Before setting V from phi")

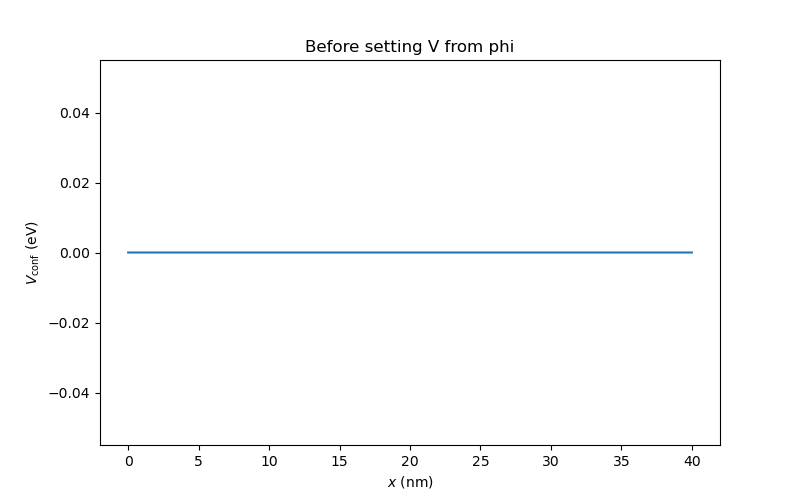
Fig. 6.4.2 Band alignment before setting the confinement potential

We see that, by default, there is no confinement potential in the device.

We then set the confined carriers to be electrons, and call set_V_from_phi to set the confinement potential from the conduction band edge.

# View the total confinement potential after calling set_V_from_phi
dvc.set_V_from_phi()
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)",
   title="After setting V from phi")

Fig. 6.4.3 Band alignment after setting the confinement potential

We see that this corresponds to the conduction band edge in Fig. 6.4.1.

6.4.5. Setting an external potential

We may set an external potential using the set_Vext method of the Device class. Here, we shift the barrier heights by \(0.5\textrm{ eV}\) upwards with

# Set an external potential to shift the barriers by +0.5 eV
dvc.set_Vext(0.5*ct.e, "left_barrier")
dvc.set_Vext(0.5*ct.e, "right_barrier")
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)",
   title="Shifted barrier heights")

This results in

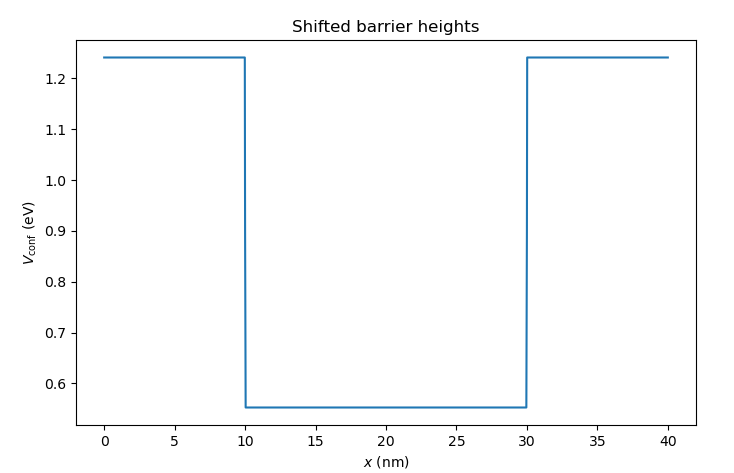
Fig. 6.4.4 Total confinement potential with barriers shifted upwards by \(0.5\textrm{ eV}\)

We may then remove the above external potential with

# Unset the external potential
dvc.set_Vext(0.0, "left_barrier")
dvc.set_Vext(0.0, "right_barrier")

6.4.6. Using band alignment parameters from RESCU+

As mentioned in the Band alignment from atomistic simulations section of this documentation, band alignment parameters can be calculated from atomistic simulations. The atomistic band alignment parameters for the GaAs/AlGaAs heterojunction are stored in the materials module, and may be activated by calling the align_bands method of the Device class, with the GaAs material as the reference material (input argument).

# Use RESCU+ simulation inputs to align bands from atomistic simulations
dvc.align_bands(mt.GaAs)
an.plot_bands(dvc, title="Band alignment from RESCU+ simulations")

This results in the following band diagram

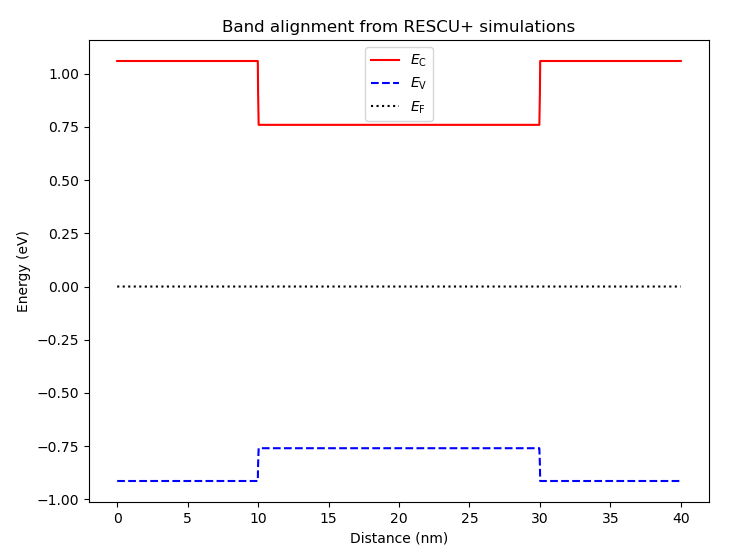
Fig. 6.4.5 Band diagram obtained using atomistic band alignment parameters evaluated with RESCU+

We see that the band diagram is slightly different from the one obtained using Anderson’s rule, which is illustrated in Fig. 6.4.1.

6.4.7. Calculating and plotting envelope functions

To calculate envelope functions, we first set the confinement potential to correspond to the band diagram illustrated above. We then instantiate the Schrödinger solver on the device, solve Schrödinger’s equation, and print the resulting eigenenergies.

# Calculate the electron envelope functions
dvc.set_V_from_phi()
slv = Solver(dvc)
slv.solve()
dvc.print_energies()

The resulting energies are

Energy levels (eV)
[0.76997686 0.80131405 0.85313421 0.92433784 1.01099512 1.06706163
1.07137673 1.10643078 1.14911842 1.17786023]

while the minimum and maximum of the conduction band edge are 0.76 eV and 1.06 eV, respectively. This means that five bound state can be obtained in this potential well. We inspect these states by plotting some of the envelope functions with

# Plot the first few levels
x = mesh.glob_nodes[:,0]
sort_indices = np.argsort(x)    # Sort the nodes along x
fig = plt.figure(figsize=(8,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("$x$ (nm)")
ax.set_ylabel("$\psi(x)$")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,0],
   "-k", label="Ground state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,1],
   "--b", label="1st excited state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,2],
   ":r", label="2nd excited state")
ax.legend()
plt.show()

which gives

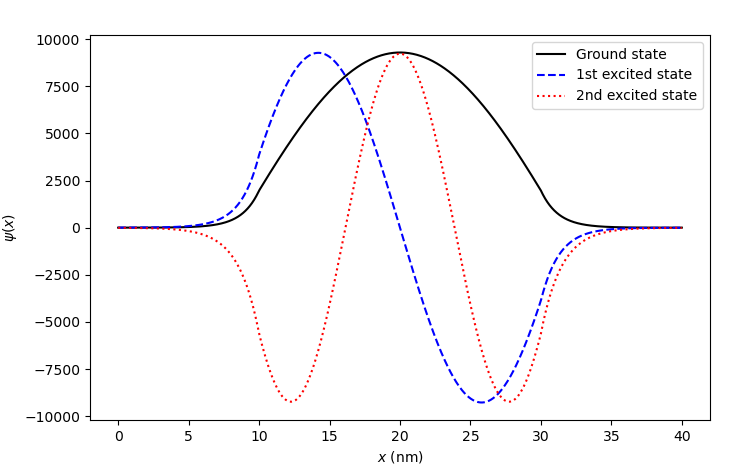
Fig. 6.4.6 Bound states in a potential well

We see that all these states look like the eigenstates of a rectangular potential well. By contrast with the eigenstates of an infinite potential well, these envelope functions penetrate slightly into the barrier regions.

We may verify that a deeper potential well results in more bound states by shifting the bands by 0.5 eV downwards in the well region. This is done by shifting the reference potential \(\varphi_F\) with the add_to_ref_potential method of the Device class. Shifting the bands and plotting the result with

# Shift the bands downwards by 0.5 eV
dvc.add_to_ref_potential(-0.5, region="well")
an.plot_bands(dvc,
   title="Band alignment from RESCU+ simulations with -0.5eV shift in well")

results in

Fig. 6.4.7 Band diagram obtained using atomistic band alignment parameters evaluated with RESCU+, with the potential well shifted by 0.5 eV downwards

We can then update the confinement potential, instantiate a new Schrödinger solver, and solve again

# Update the confinement potential and solve Schrodinger again
dvc.set_V_from_phi()
slv = Solver(dvc)
slv.solve()
dvc.print_energies()

The resulting eigenenergies are then

Energy levels (eV)
[0.27117749 0.30618482 0.36443591 0.4457467  0.54975075 0.67569868
0.82186199 1.0685614  1.12593835 1.19666353]

We see that seven energy levels now lie between the conduction band minimum (0.26 eV) and maximum (1.06 eV).

Plotting the electron envelope functions, we see that we indeed have bound states which look essentially like those of the previous potential well.

# Plot the first few levels again
x = mesh.glob_nodes[:,0]
sort_indices = np.argsort(x)    # Sort the nodes along x
fig = plt.figure(figsize=(8,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("$x$ (nm)")
ax.set_ylabel("$\psi(x)$")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,0],
   "-k", label="Ground state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,1],
   "--b", label="1st excited state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,2],
   ":r", label="2nd excited state")
ax.legend()
plt.show()

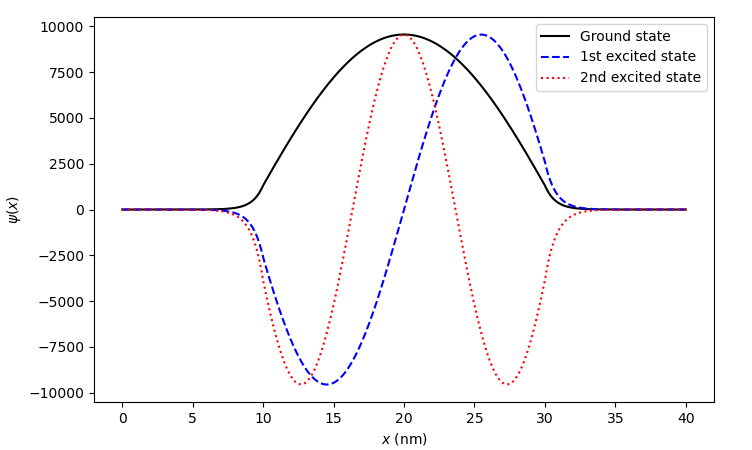
Fig. 6.4.8 Bound states in an artificially deeper potential well

6.5. Full code

__copyright__ = "Copyright 2022-2024, Nanoacademic Technologies Inc."

import numpy as np
from matplotlib import pyplot as plt
from pathlib import Path
from qtcad.device import constants as ct
from qtcad.device.mesh1d import Mesh
from qtcad.device import Device
from qtcad.device import materials as mt
from qtcad.device import analysis as an
from qtcad.device.schrodinger import Solver

# Path to mesh file
path = Path(__file__).parent.resolve()
path = path / "meshes" / "band_alignment.msh"

# Load the mesh
mesh = Mesh(1e-9,path)

# Create the device and add materials
dvc = Device(mesh, conf_carriers="e")

dvc.new_region("left_barrier", mt.AlGaAs)
dvc.new_region("well", mt.GaAs)
dvc.new_region("right_barrier", mt.AlGaAs)

# Show the band diagram obtained from Anderson's rule
an.plot_bands(dvc, title="Anderson's rule")

# View the total confinement potential before calling set_V_from_phi
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)", 
   title="Before setting V from phi")

# View the total confinement potential after calling set_V_from_phi
dvc.set_V_from_phi()
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)", 
   title="After setting V from phi")

# Set an external potential to shift the barriers by +0.5 eV
dvc.set_Vext(0.5*ct.e, "left_barrier")
dvc.set_Vext(0.5*ct.e, "right_barrier")
an.plot(mesh, dvc.get_Vconf()/ct.e, ylabel="$V_\mathrm{conf}$ (eV)", 
   title="Shifted barrier heights")

# Unset the external potential
dvc.set_Vext(0.0, "left_barrier")
dvc.set_Vext(0.0, "right_barrier")

# Use RESCU+ simulation inputs to align bands from atomistic simulations
dvc.align_bands(mt.GaAs)
an.plot_bands(dvc, title="Band alignment from RESCU+ simulations")

# Calculate the electron envelope functions
dvc.set_V_from_phi()
slv = Solver(dvc)
slv.solve()
dvc.print_energies()

# Plot the first few levels
x = mesh.glob_nodes[:,0]
sort_indices = np.argsort(x)    # Sort the nodes along x
fig = plt.figure(figsize=(8,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("$x$ (nm)")
ax.set_ylabel("$\psi(x)$")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,0],
   "-k", label="Ground state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,1],
   "--b", label="1st excited state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,2],
   ":r", label="2nd excited state")
ax.legend()
plt.show()

# Shift the bands downwards by 0.5 eV
dvc.add_to_ref_potential(-0.5, region="well")
an.plot_bands(dvc, 
   title="Band alignment from RESCU+ simulations with -0.5eV shift in well")

# Update the confinement potential and solve Schrodinger again
dvc.set_V_from_phi()
slv = Solver(dvc)
slv.solve()
dvc.print_energies()

# Plot the first few levels again
x = mesh.glob_nodes[:,0]
sort_indices = np.argsort(x)    # Sort the nodes along x
fig = plt.figure(figsize=(8,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel("$x$ (nm)")
ax.set_ylabel("$\psi(x)$")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,0],
   "-k", label="Ground state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,1],
   "--b", label="1st excited state")
ax.plot(x[sort_indices]/1e-9, dvc.eigenfunctions[sort_indices,2],
   ":r", label="2nd excited state")
ax.legend()
plt.show()