14. Many-body analysis of a nanowire quantum dot

14.1. Requirements

14.1.1. Software components

  • qtcad

  • gmsh

14.1.2. Geometry file

  • qtcad/examples/tutorials/meshes/nanowire.geo

14.1.3. Python script

  • qtcad/examples/tutorials/manybody.py

14.1.4. References

14.2. Briefing

In this tutorial, we build on the results output in the Poisson and Schrödinger simulation of a nanowire quantum dot tutorial (see Python script qtcad/examples/tutorials/nanowire.py). Loading the potential obtained at the end of this file, we solve the many-body problem for a system consisting of a few electrons confined in the potential well formed by the conduction band edge within the channel of the nanowire quantum dot. We then illustrate the various physical outputs that can be extracted from the many-body solution.

14.3. Setting up the device and loading results from the previous simulation

14.3.2. Creating the device

We next load the mesh, instantiate the device, and set up regions and boundary conditions exactly as in the previous tutorial.

# Define some device parameters
Vgs = 0.5 # Gate-source bias
Ew = mt.Si.chi + mt.Si.Eg/2 # Metal work function
Ltot = 20e-9 # Device height in m
radius = 2.5e-9 # Device radius in m

# Paths to mesh file and output files
script_dir = pathlib.Path(__file__).parent.resolve()
path_mesh = script_dir / "meshes/" / "nanowire.msh"
path_hdf5 = script_dir / "output/" / "nanowire.hdf5"

# Load the mesh
scaling = 1e-9
mesh = Mesh(scaling, str(path_mesh))

# Create device from mesh and set statistics.
# It is important to set statistics before creating boundaries since
# they determine the boundary values, Failing to do so will produce
# inconsistent results.
dvc = Device(mesh, conf_carriers="e")
dvc.statistics = "FD_approx"  # Analytic approximation to Fermi-Dirac statistics

# Create regions first.
# Make sure each element is assigned to a region, otherwise default
# (silicon) parameters are used
dvc.new_region('channel_ox',mt.SiO2)
dvc.new_region('source_ox',mt.SiO2)
dvc.new_region('drain_ox',mt.SiO2)
dvc.new_region('channel', mt.Si)
dvc.new_region('source', mt.Si, pdoping=5e20*1e6, ndoping=0)
dvc.new_region('drain', mt.Si, pdoping=5e20*1e6, ndoping=0)

# Then create boundaries
dvc.new_ohmic_bnd('source_bnd')
dvc.new_ohmic_bnd('drain_bnd')
dvc.new_gate_bnd('gate_bnd',Vgs,Ew)

The next step is to load the electric potential from the hdf5 output file produced in the previous tutorial.

# Load the electic potential
dvc.set_potential(io.load(path_hdf5,"phi"))

It is important to use the set_potential method of the Device class rather than modifying the phi attribute directly because the method automatically recalculates the potential energy V.

14.4. Solving the many-body problem

We first solve the single-electron problem, which will define the single-particle basis set for the many-body problem

# Solve the single-electron problem
slv = SingleBodySolver(dvc)
slv.solve()
dvc.print_energies()

The single-particle energies will be output as

Energy levels (eV)
[0.54798018 0.61320021 0.68496646 0.76317642 0.8478653  0.93920254
1.03757746 1.14369621 1.15198013 1.15240696]

We then instantiate and run the many-body Solver.

# Solve the many-body problem
solver_params = SolverParams()
solver_params.num_states = 3
solver_params.n_degen = 2
solver_params.alpha = 0.5
solver_params.num_particles = [0,1,2,3]
slv = ManyBodySolver(dvc, solver_params = solver_params)
slv.solve()

Here we limit the number of single-particle orbitals to consider in the basis set to \(3\), and set the degeneracy of these orbitals to \(2`\) (e.g. from spin). In addition, we introduce a lever arm \(\alpha\) of \(0.5\). The lever arm quantifies the extent by which a potential applied at a gate can shift the energy-level structure of the device (see the lever arm Theory section). Finally, we set the num_particles attribute of the many-body SolverParams to a list of integers \(N\) labeling the \(N\)-particle subspaces to consider. Here, we choose to only consider the 0-, 1-, 2-, and 3-particle subspaces even though for \(n_\mathrm{states} = 3\) and \(n_\mathrm{degen} = 2\), the maximum number of particles that can be considered in principle is \(n_\mathrm{states} \times n_\mathrm{degen} = 6\). This choice is up to the user, but taking a smaller number of particles than the total accessible amount will typically make calculations faster.

After calling the solve method, progress bars appear to track the calculation of Coulomb integrals

Initializing Coulomb matrix calculation. ████████████████████████████████ 100%
Computing contributions to block-row 0 (part 1/2) ████████████████████████████████ 100%
Computing contributions to block-row 1 (part 1/2) ████████████████████████████████ 100%
Computing contributions to block-row 2 (part 1/2) ████████████████████████████████ 100%
Computing contributions to block-row 0 (part 2/2) ████████████████████████████████ 100%
Computing contributions to block-row 1 (part 2/2) ████████████████████████████████ 100%
Computing contributions to block-row 2 (part 2/2) ████████████████████████████████ 100%
Computing Coulomb integrals...
Done.

14.5. Analyzing the results

Once the calculation is done, we produce various outputs that are made available through quantities stored as new Device attributes.

14.5.1. Many-body subspace properties

We first analyze the many-body subspaces with

# Many-body subspace properties
print("Many-body subspaces:", dvc.many_body_subspaces)
print("Number of subspaces:", len(dvc.many_body_subspaces))
print("Electron number in subspace 2:", dvc.many_body_subspaces[2].N)

which results in

Many-body subspaces: [<device.core.quantum.Subspace object at 0x00000215769AD6A0>, <device.core.quantum.Subspace object at 0x0000021576CC1E80>, <device.core.quantum.Subspace object at 0x0000021576CC1FA0>, <device.core.quantum.Subspace object at 0x0000021576CC1E20>]
Number of subspaces: 4
Electron number in subspace 2: 2

In general, for \(n_\mathrm{states}=3\) single-particle orbitals with degeneracy \(n_\mathrm{degen}=2\), we have \(n_\mathrm{states}\times n_\mathrm{degen}+1=7\) subspaces corresponding to \(0\) to \(N_\mathrm{max}=n_\mathrm{states}\times n_\mathrm{degen}=6\) electrons (see Exact diagonalization). However, here, we have kept only the 0, 1, 2, and 3-electron subspaces. With these subspace integer labels starting at 0, the many-body subspace with index 2 is indeed expected to involve 2 electrons, as seen above.

Each subspace contains a many-body basis set. For example, the two-electron subspace basis set is displayed with

print("Two-electron many-body basis set (integers): ")
print(dvc.get_N_particle_subspace(2).get_bas_set())

which results in

Two-electron many-body basis set (integers):
[ 3  5  9 17 33  6 10 18 34 12 20 36 24 40 48]

By default, each many-body basis state is labeled by an integer whose binary representation gives the occupation (0 if unoccupied, 1 if occupied) of each single-partical orbital (see the get_bas_set API reference). This is the most compact representation available in QTCAD in terms of memory usage. The strings for these binaries may be displayed with:

print("Two-electron many-body basis set (binary strings): ")
print(dvc.get_N_particle_subspace(2).get_bas_set(dtype="str"))

which results in

Two-electron many-body basis set (binary strings):
['000011' '000101' '001001' '010001' '100001' '000110' '001010' '010010'
'100010' '001100' '010100' '100100' '011000' '101000' '110000']

We remark that these strings must be read from right to left when converting into orbital occupations. The above basis set may be written as an array of integers whose rows correspond to many-body basis states and columns to single-particle orbitals with

print("Two-electron many-body basis set (array): ")
print(dvc.get_N_particle_subspace(2).get_bas_set(dtype="array"))

which results in

Two-electron many-body basis set (array):

[[1 1 0 0 0 0]
[1 0 1 0 0 0]
[1 0 0 1 0 0]
[1 0 0 0 1 0]
[1 0 0 0 0 1]
[0 1 1 0 0 0]
[0 1 0 1 0 0]
[0 1 0 0 1 0]
[0 1 0 0 0 1]
[0 0 1 1 0 0]
[0 0 1 0 1 0]
[0 0 1 0 0 1]
[0 0 0 1 1 0]
[0 0 0 1 0 1]
[0 0 0 0 1 1]]

This corresponds to all possible occupancy configurations of the \(n_\mathrm{states}\times n_\mathrm{degen}=6\) single-particle orbitals in which the total number of electrons is \(2\).

We can also display the many-body eigenvalues for a specific subspace, here the two-electron subspace, with

print("Two-electron many-body eigenvalues (eV): ")
print(dvc.get_N_particle_subspace(2).eigval/ct.e)

which yields

Two-electron many-body eigenvalues (eV):
[1.1866333  1.21956697 1.21956697 1.21956697 1.26025576 1.29465441
1.29465441 1.29465441 1.29522516 1.33092987 1.3533585  1.3533585
1.3533585  1.39007039 1.44432475]

In addition, we can display, e.g., the first two-electron eigenstates with

print("Two-electron many-body ground state:")
print(dvc.get_N_particle_subspace(2).eigvec[:,0])
print("Two-electron many-body first excited state:")
print(dvc.get_N_particle_subspace(2).eigvec[:,1])

which produces

Two-electron many-body ground state:
[ 9.62702118e-01 -5.82867088e-15 -1.72484631e-04 -2.34187669e-17
1.34633424e-01  1.72484631e-04 -1.30162049e-29 -1.34633424e-01
-1.00148357e-32 -1.90808684e-01  5.71304700e-16 -2.01203414e-06
2.01203414e-06  1.28440684e-30 -2.33302740e-02]
Two-electron many-body first excited state:
[ 7.85439690e-15  9.77357445e-01 -4.48217994e-02 -4.46877504e-05
2.04938878e-06 -4.48217994e-02  1.60967022e-01  2.04938879e-06
-7.35990107e-06  3.26308111e-15 -1.19971249e-01  5.50190442e-03
5.50190442e-03 -1.97588045e-02 -1.67237142e-16]

As can be seen from above, the two-body eigenstates are superpositions of the many-body basis states. We remark that because the two-body excited states are degenerate in this example, the two-body first excited states span a Hilbert space. The specific combination of coefficients in the first excited state displayed above is but one of the infinite potential linear combinations that exist within this Hilbert space. This specific outcome is determined by the eigenvalue solver and may thus differ between machines or QTCAD versions.

In the trivial case of the single-body subspace, the basis states are also many-body eigenstates. This can be verified with

print("One-electron many-body basis set:")
print(dvc.get_N_particle_subspace(1).get_bas_set(dtype="array"))
print("One-electron many-body eigenstates:")
print(dvc.get_N_particle_subspace(1).eigvec)

which produces

One-electron many-body basis set:
[[1 0 0 0 0 0]
[0 1 0 0 0 0]
[0 0 1 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 1]]
One-electron many-body eigenstates:
[[1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 1.]]

Also, remark that information about the many-body eigenstates and energies can be equivalently obtained through the get_eig_state method, which outputs an MbState object capturing all the physical information about a many-body state. For example, we can display the two-electron ground-state coefficients (of the expansion over the many-body basis) and energy with

# Many-body state objects
print("Two-electron ground-state coefficients and energy (eV)")
print(dvc.get_N_particle_subspace(2).get_eig_state(0).coeff)
print(dvc.get_N_particle_subspace(2).get_eig_state(0).energy/ct.e)

which results in

Two-electron ground-state coefficients and energy (eV)
[ 9.62702118e-01 -5.82867088e-15 -1.72484631e-04 -2.34187669e-17
1.34633424e-01  1.72484631e-04 -1.30162049e-29 -1.34633424e-01
-1.00148357e-32 -1.90808684e-01  5.71304700e-16 -2.01203414e-06
2.01203414e-06  1.28440684e-30 -2.33302740e-02]
1.1866333005439096

14.5.2. Chemical potentials and Coulomb peak positions

We next output the chemical potentials and Coulomb peak positions for this device and gate bias configuration (see Chemical potentials and Coulomb peak positions).

This is done with

# Chemical potentials and Coulomb peak positions
print("Chemical potentials (eV)")
print(dvc.chem_potentials/ct.e)
print("Coulomb peak positions (V)")
print(dvc.coulomb_peak_pos)

which yields

Chemical potentials (eV)
[0.54798018 0.63865312 0.750661  ]
Coulomb peak positions (V)
[1.09596035 1.27730625 1.501322  ]

Because we have taken the lever arm \(\alpha\) to be \(0.5\), the position of the Coulomb peaks is twice the chemical potentials.

Note

The position of the Coulomb peaks is given relative to the reference gate potential. The reference gate potential is the potential applied at the boundary condition when solving Poisson’s equation.

For example, at vanishing source–drain bias, to see the Coulomb peak associated with the transition from \(0\) to \(1\) electron inside the potential well in the nanowire channel, a gate bias of \(V_\mathrm{GS}+\mu(1)/e\alpha = 0.5\;\mathrm V+0.54798\;\mathrm V/0.5 = 1.59596\;\mathrm V\) would need to be applied for a lever arm \(\alpha=0.5\).

14.5.3. Many-body particle density

Finally, we may plot the particle densities associated with many-body eigenstates of interest as follows.

# Plot electron density
an.plot_slices(mesh, dvc.get_many_body_density(1,0),
    title="One-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(1,2),
    title="One-electron second-excited state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(2,0),
    title="Two-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(2,2),
    title="Two-electron second-excited state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(3,0),
    title="Three-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(3,5),
    title="Three-electron fifth-excited state particle density (1/m^3)")

The resulting plots are shown below.

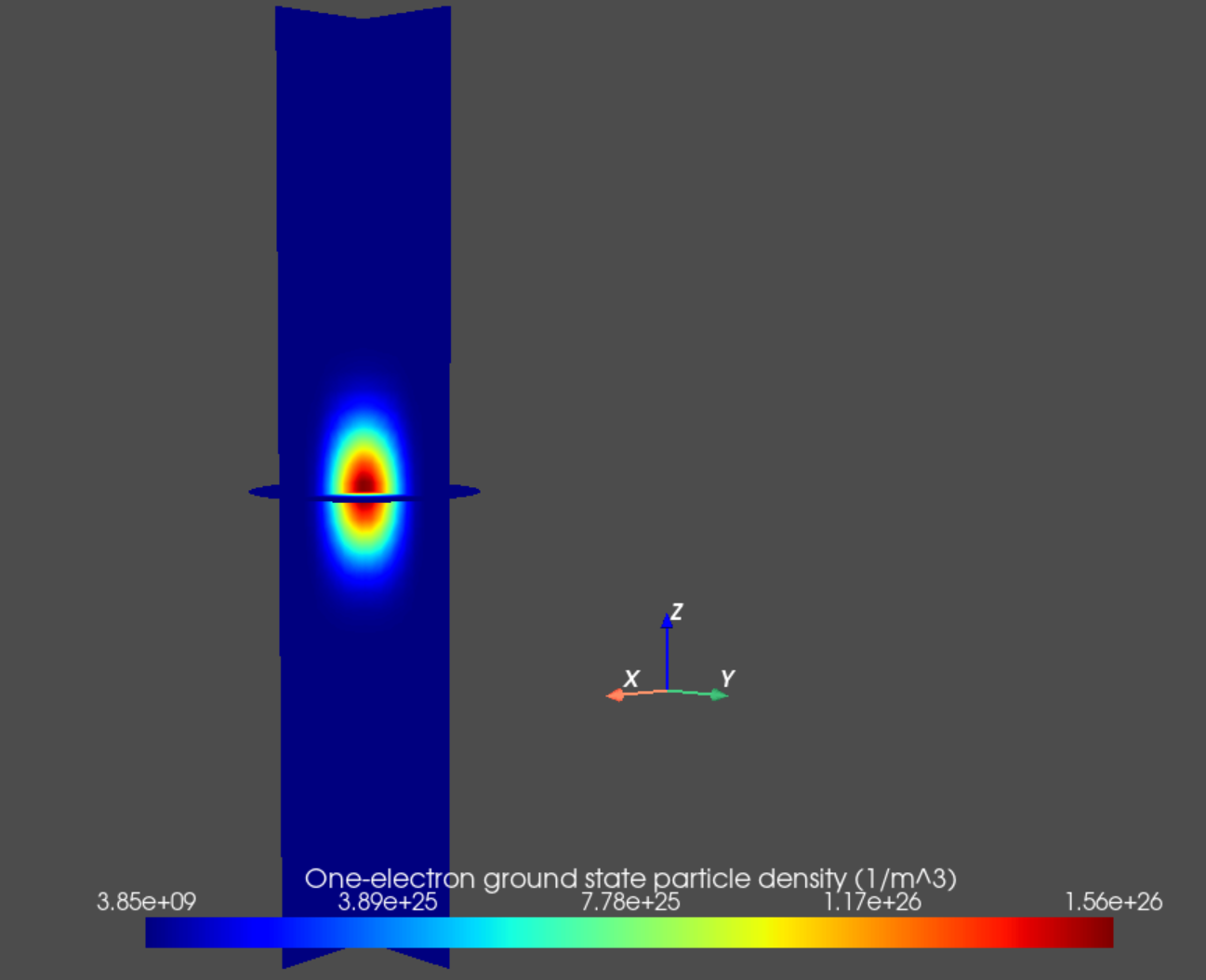
One-electron ground state particle density

Fig. 14.5.1 One-electron ground state particle density

One-electron second excited state

Fig. 14.5.2 One-electron second excited state particle density

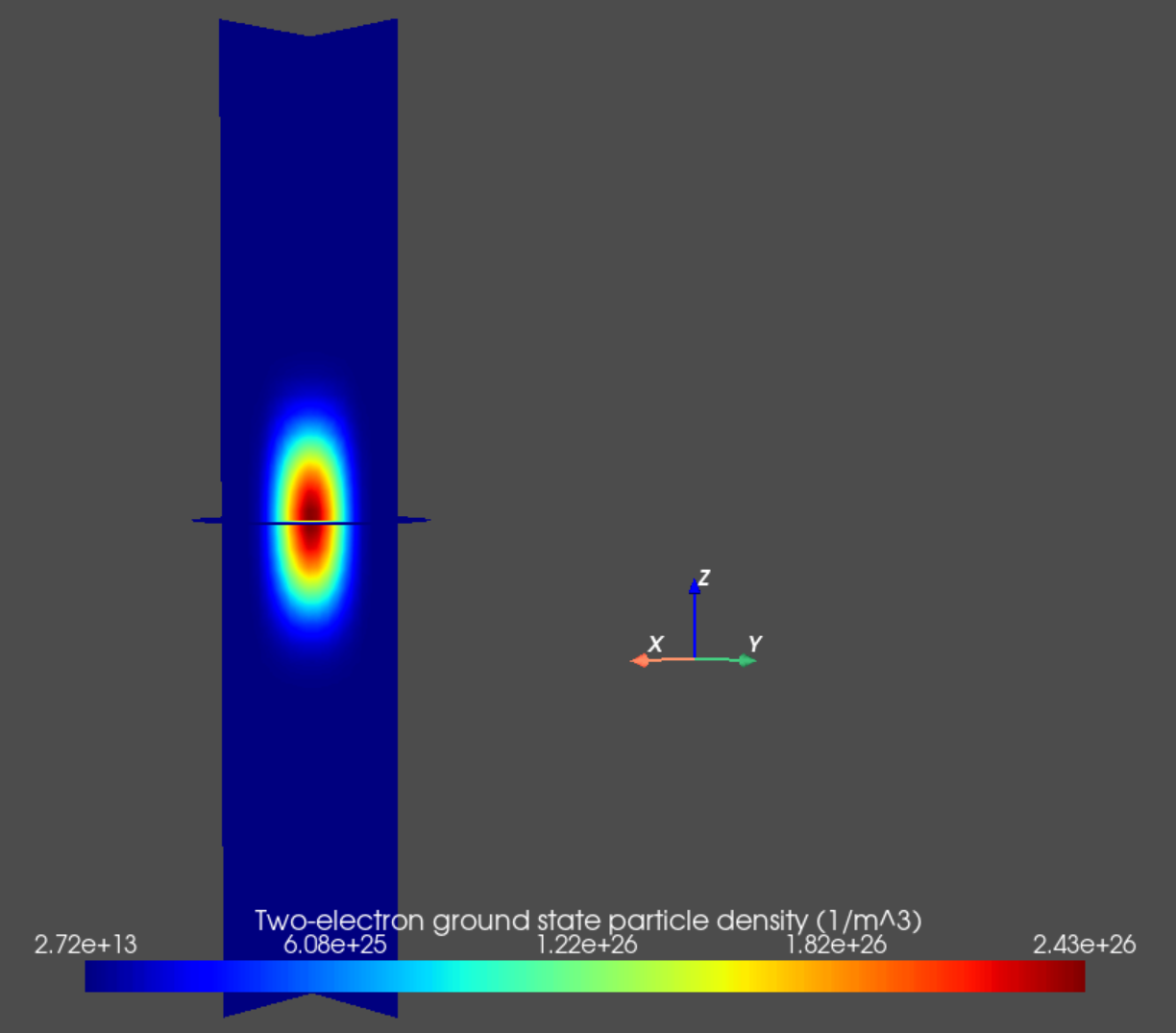
Two-electron ground state

Fig. 14.5.3 Two-electron ground state particle density

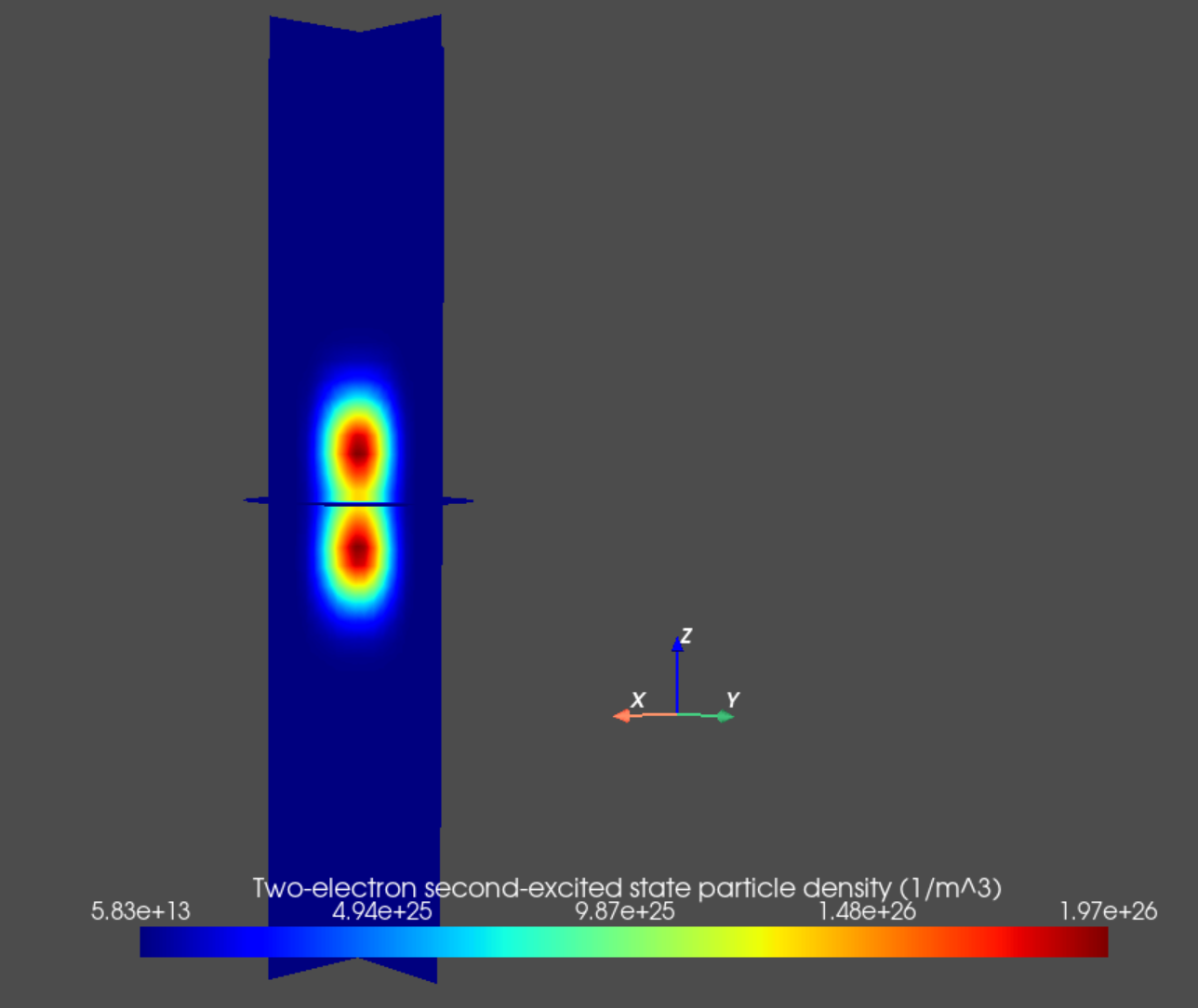
Two-electron second excited state

Fig. 14.5.4 Two-electron second excited state particle density

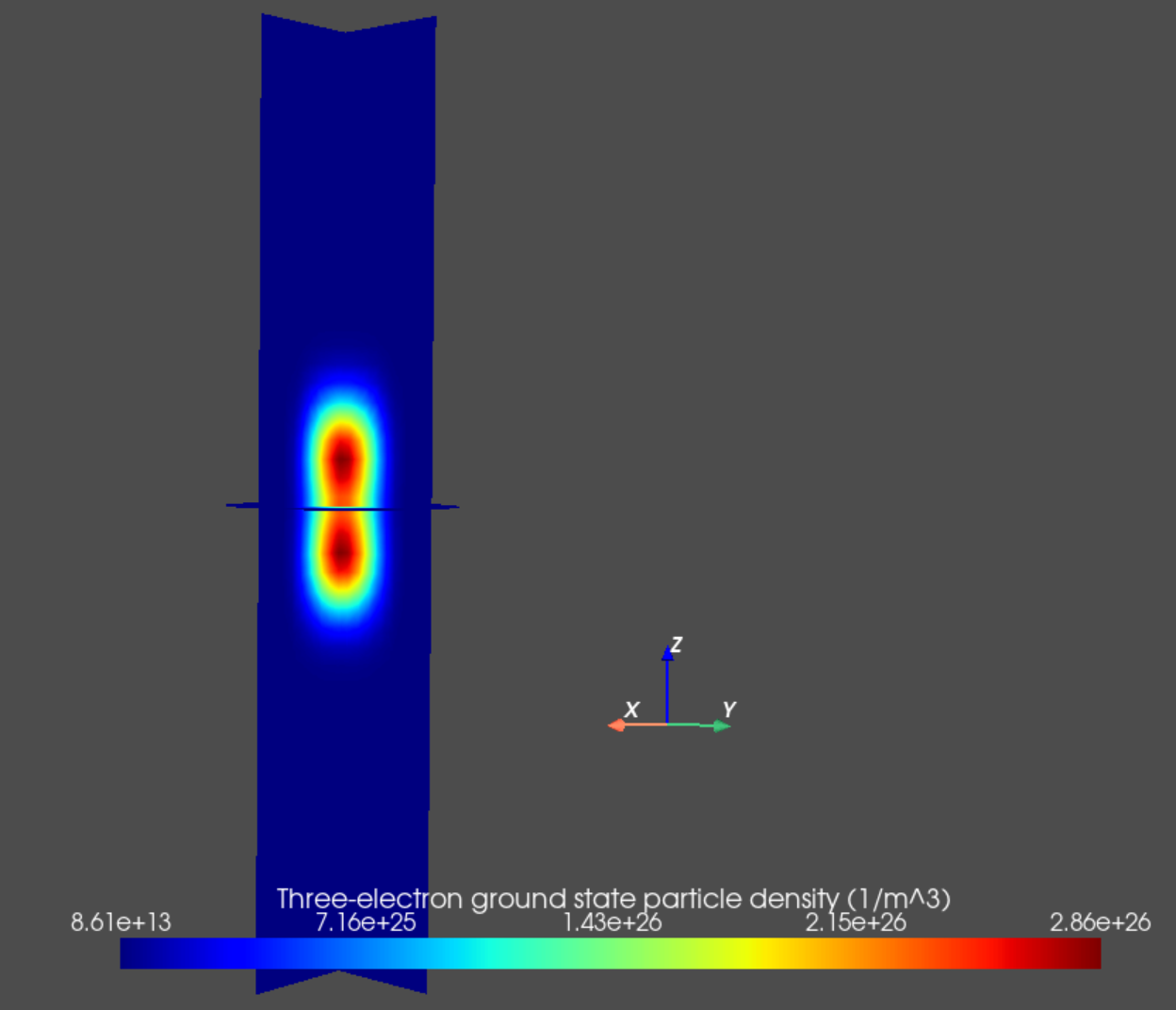
Three-electron ground state

Fig. 14.5.5 Three-electron ground state particle density

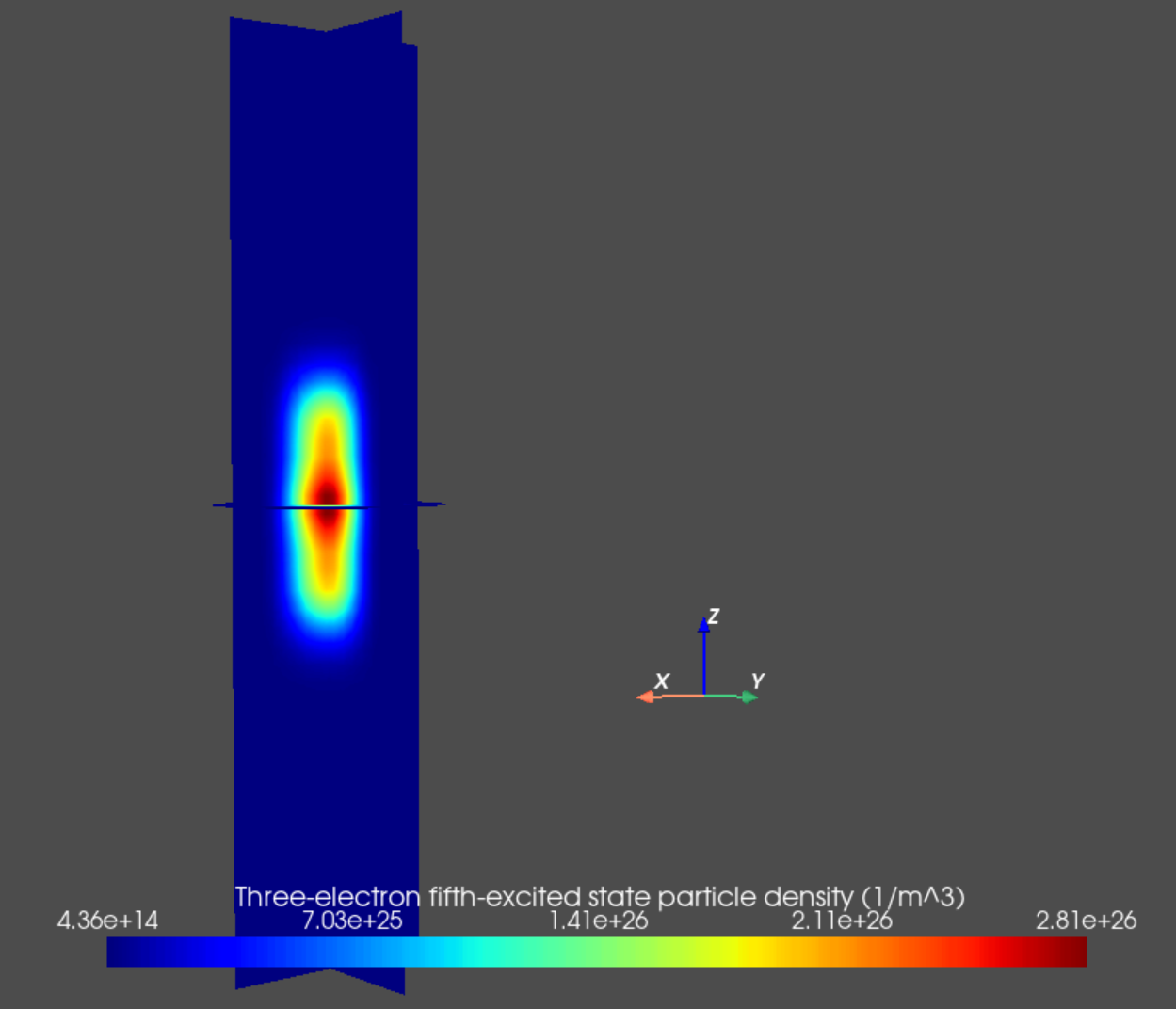
Three-electron fifth excited state

Fig. 14.5.6 Three-electron fifth excited state particle density

Note

The Subspace objects stored in the many_body_subspaces of a Device object account for single-particle state degeneracy explicitly. As a result, in this example, the particle density of the first single-electron “excited” state is the same as for the single-electron ground state, simply because these states are taken to be degenerate. Therefore, the first single-electron eigenstate whose particle density differs from the ground state is the one with eigenstate label \(2\).

14.6. Full code

__copyright__ = "Copyright 2022-2024, Nanoacademic Technologies Inc."

from qtcad.device import constants as ct
from qtcad.device.mesh3d import Mesh
from qtcad.device import io
from qtcad.device import analysis as an
from qtcad.device import materials as mt
from qtcad.device import Device
from qtcad.device.schrodinger import Solver as SingleBodySolver
import pathlib
from qtcad.device.many_body import Solver as ManyBodySolver
from qtcad.device.many_body import SolverParams

# Define some device parameters
Vgs = 0.5 # Gate-source bias
Ew = mt.Si.chi + mt.Si.Eg/2 # Metal work function
Ltot = 20e-9 # Device height in m
radius = 2.5e-9 # Device radius in m

# Paths to mesh file and output files
script_dir = pathlib.Path(__file__).parent.resolve()
path_mesh = script_dir / "meshes/" / "nanowire.msh"
path_hdf5 = script_dir / "output/" / "nanowire.hdf5"

# Load the mesh
scaling = 1e-9
mesh = Mesh(scaling, str(path_mesh))

# Create device from mesh and set statistics.
# It is important to set statistics before creating boundaries since
# they determine the boundary values, Failing to do so will produce
# inconsistent results.
dvc = Device(mesh, conf_carriers="e")
dvc.statistics = "FD_approx"  # Analytic approximation to Fermi-Dirac statistics

# Create regions first.
# Make sure each element is assigned to a region, otherwise default
# (silicon) parameters are used
dvc.new_region('channel_ox',mt.SiO2)
dvc.new_region('source_ox',mt.SiO2)
dvc.new_region('drain_ox',mt.SiO2)
dvc.new_region('channel', mt.Si)
dvc.new_region('source', mt.Si, pdoping=5e20*1e6, ndoping=0)
dvc.new_region('drain', mt.Si, pdoping=5e20*1e6, ndoping=0)

# Then create boundaries
dvc.new_ohmic_bnd('source_bnd')
dvc.new_ohmic_bnd('drain_bnd')
dvc.new_gate_bnd('gate_bnd',Vgs,Ew)

# Load the electic potential
dvc.set_potential(io.load(path_hdf5,"phi"))

# Solve the single-electron problem
slv = SingleBodySolver(dvc)
slv.solve()
dvc.print_energies()

# Solve the many-body problem
solver_params = SolverParams()
solver_params.num_states = 3
solver_params.n_degen = 2
solver_params.alpha = 0.5
solver_params.num_particles = [0,1,2,3]
slv = ManyBodySolver(dvc, solver_params = solver_params)
slv.solve()

# Many-body subspace properties
print("Many-body subspaces:", dvc.many_body_subspaces)
print("Number of subspaces:", len(dvc.many_body_subspaces))
print("Electron number in subspace 2:", dvc.many_body_subspaces[2].N)

print("Two-electron many-body basis set (integers): ")
print(dvc.get_N_particle_subspace(2).get_bas_set())

print("Two-electron many-body basis set (binary strings): ")
print(dvc.get_N_particle_subspace(2).get_bas_set(dtype="str"))

print("Two-electron many-body basis set (array): ")
print(dvc.get_N_particle_subspace(2).get_bas_set(dtype="array"))

print("Two-electron many-body eigenvalues (eV): ")
print(dvc.get_N_particle_subspace(2).eigval/ct.e)

print("Two-electron many-body ground state:")
print(dvc.get_N_particle_subspace(2).eigvec[:,0])
print("Two-electron many-body first excited state:")
print(dvc.get_N_particle_subspace(2).eigvec[:,1])

print("One-electron many-body basis set:")
print(dvc.get_N_particle_subspace(1).get_bas_set(dtype="array"))
print("One-electron many-body eigenstates:")
print(dvc.get_N_particle_subspace(1).eigvec)

# Many-body state objects
print("Two-electron ground-state coefficients and energy (eV)")
print(dvc.get_N_particle_subspace(2).get_eig_state(0).coeff)
print(dvc.get_N_particle_subspace(2).get_eig_state(0).energy/ct.e)

# Chemical potentials and Coulomb peak positions
print("Chemical potentials (eV)")
print(dvc.chem_potentials/ct.e)
print("Coulomb peak positions (V)")
print(dvc.coulomb_peak_pos)

# Plot electron density
an.plot_slices(mesh, dvc.get_many_body_density(1,0),
    title="One-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(1,2),
    title="One-electron second-excited state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(2,0),
    title="Two-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(2,2),
    title="Two-electron second-excited state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(3,0),
    title="Three-electron ground state particle density (1/m^3)")
an.plot_slices(mesh, dvc.get_many_body_density(3,5),
    title="Three-electron fifth-excited state particle density (1/m^3)")